粒子算法在目标跟踪参数估计与模型选择中的应用

需积分: 9 56 浏览量更新于2024-09-14 收藏 310KB PDF 举报

"这篇资料主要涉及目标跟踪领域的算法，特别是视频目标跟踪技术。文中提到了一种用于序列贝叶斯参数估计和模型选择的粒子算法，由Dominic S. Lee和Nicholas K. K. Chia撰写，发表在2002年的IEEE Transactions on Signal Processing期刊第50卷第2期上。" 本文的核心是介绍了一种创新的粒子算法，该算法旨在解决序列贝叶斯估计中的计算效率和稳定性问题。贝叶斯估计是一种统计方法，它利用先验知识和观测数据来估计未知参数。在目标跟踪中，这通常涉及到动态地更新对目标位置、速度等属性的估计。首先，算法采用顺序重要性采样（Sequential Importance Sampling, SIS），这是一种在处理测量数据时更新概率分布的方法。SIS通过生成一组代表概率分布的粒子，并根据新测量值重新权重这些粒子，从而提供对参数的近似估计。由于粒子数量有限，这种方法可能会引入误差，但其计算成本较低。接着，为了克服SIS的累积误差问题，论文提出了一个再生成测试（rejuvenation test）。这个测试在每次处理完一个测量值后检查粒子是否需要更新。如果需要，粒子将通过马尔科夫链蒙特卡洛（Markov Chain Monte Carlo, MCMC）进行完全更新，这有助于消除由于粒子数量有限而积累的误差，确保算法的稳定性。 MCMC是一种模拟随机过程以探索复杂概率分布的技术，它能有效地在高维空间中探索状态空间，尤其适合处理多变量或非独立的问题。在本文的算法中，MCMC不仅用于更新粒子，而且当可能时，还可以利用SIS的粒子来提高效率。最后，尽管文章没有提供完整的内容，但从摘要中可以看出，该研究还探讨了如何在MCMC步骤中有效地利用SIS的粒子，这可能涉及到粒子的重用或优化，以进一步提升算法的性能和效率。这份资料深入探讨了目标跟踪中的一种先进算法，结合了SIS和MCMC的优点，解决了传统方法中可能遇到的计算效率和稳定性挑战，对于理解和改进视频目标跟踪技术具有重要意义。

328 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 50, NO. 2, FEBRUARY 2002

for a rejuvenation test based on a Kullback–Leibler (KL) dis-

tance and with independent Metropolis–Hastings (IMH) as our

MCMC choice. We will demonstrate the stability of this par-

ticular algorithm with an application example in Section III,

involving both simulated and real data, with low SNR (about

9 dB for the simulation and 14 dB for the real data) and

with a large number of measurements (65536 measurements) in

the simulation.

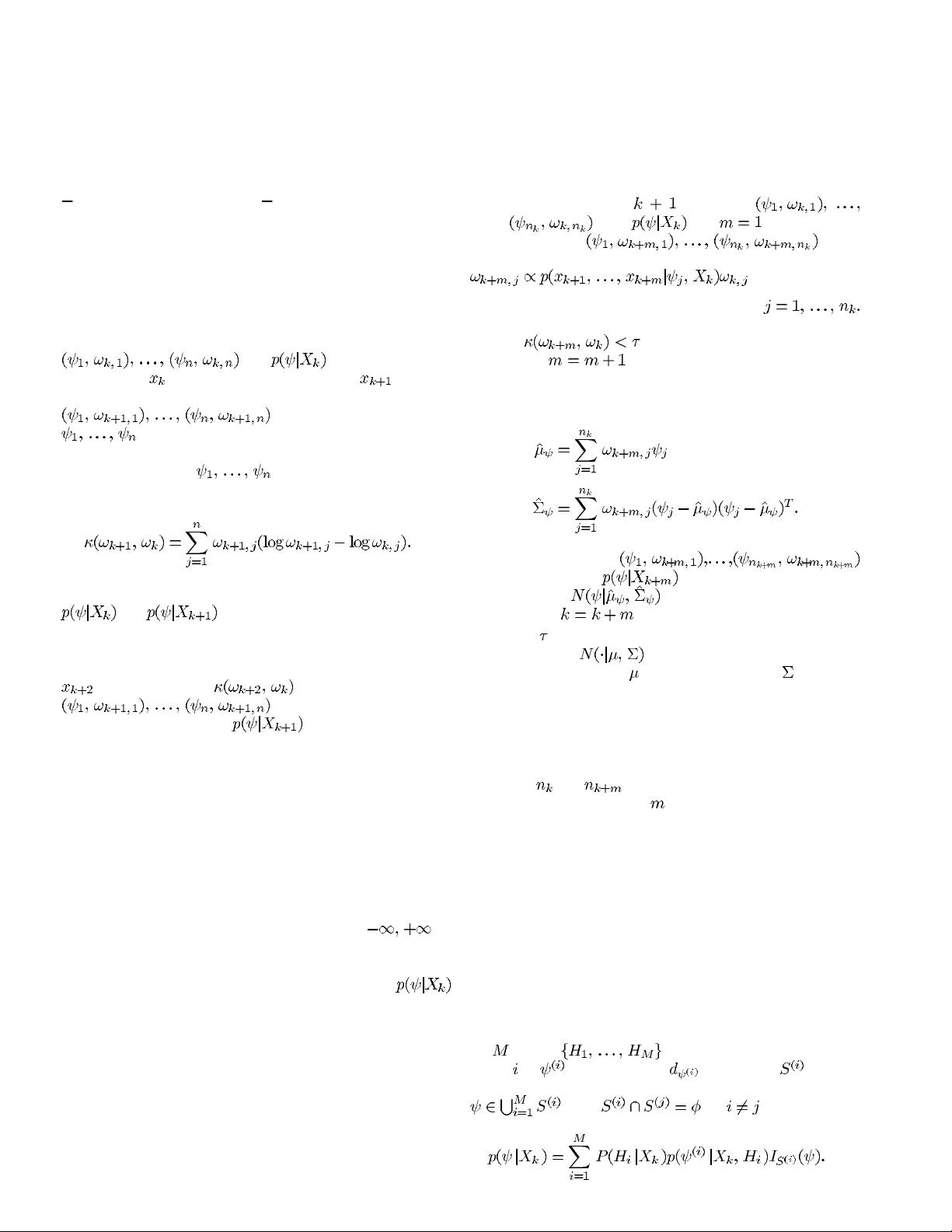
B. SMCMC Filter With KL Test and IMH

We use a rejuvenation test that is based on the idea

of a KL distance between two discrete distributions.

Suppose we have a rejuvenated set of weighted particles

for after incorporating

measurement

. When the next measurement becomes

available, the weighted particles are updated by SIS to give

. Since the particle values

themselves are not changed by SIS, we can regard

the two sets of weighted particles as discrete distributions on

the common support

, and define the KL distance

between them as

(3)

Intuitively, this measures how dissimilar the two densities,

and , are through their particle representa-

tions. Equivalently, (3) measures the amount of change in the

weights caused by the new measurement. If the densities are not

too dissimilar, we proceed with SIS for the next measurement

and then check ; otherwise, we replace

by a completely rejuvenated

set of particles drawn from

using MCMC.

Other rejuvenation tests that measure the skewness of the

weights of the particles at each time step are also possible. For

example, we can use the coefficient of variation of the weights

[12] or simply monitor the maximum weight. However, unlike

the KL test, these do not measure the change in the weights.

For simplicity, we perform MCMC using IMH (see, for ex-

ample, [17]) with a Gaussian proposal density whose mean and

covariance are computed from the most recent SIS particles.

In practice, it may be necessary to avoid underestimating the

variances for the proposal density by inflating the estimated

variances. Any parameter whose support is not (

)is

reparameterized to this support where the Gaussian proposal

density is then applied. We use the Gelman–Rubin test [7] with

two chains to monitor MCMC convergence. Since

approaches a Gaussian density asymptotically in the number of

measurements (see, for example, [18]), the Gaussian proposal

density for IMH becomes more efficient as more measurements

are processed. In the early and intermediate stages, however,

other proposal densities such as finite Gaussian mixtures or

kernel density estimators may fare better. When available,

analytical approximations to the target density can also be used

as proposal densities. A particularly attractive idea that can

be used in conjunction with any proposal density is to use a

sequence of bridging densities between the proposal density

and the target density [9]. For the applications in Section III,

the Gaussian proposal density appears to be adequate.

Using the KL rejuvenation test together with IMH with

a Gaussian proposal density, the SMCMC filter takes the

following form.

1) Start of time-step

:Wehave

from . Set .

2) SIS: Obtain

for

3) If , then

Set

. Go to Step 2.

Else

a) Compute

b) IMH: Obtain

with as target density and

as proposal density.

c) Set

. Go to Step 1.

In Step 3,

is a threshold that must be specified for the KL

test. In Step 3b),

denotes the multivariate Gaussian

density with mean vector

and covariance matrix . IMH pro-

duces particles that are possibly replicated but equally weighted.

In our notation, we are representing them as distinct particles

with unequal weights—this also helps to save on storage during

implementation. Notice that in general, the number of particles

before and after rejuvenation need not remain the same, hence,

the use of

and .

We refer to the number

between rejuvenations as the

batch size. It varies adaptively depending on the outcome of

the rejuvenation test. Bigger batches mean that MCMC is

performed less frequently. In practice, we observe an exponen-

tially increasing trend in the batch size over time, suggesting

that real-time implementation of the SMCMC filter is feasible.

C. Simultaneous Model Selection and Parameter Estimation

To perform simultaneous model selection and parameter esti-

mation with the SMCMC filter, we simply use multiple models

together with a suitable MCMC method that allows transitions

between parameter spaces whose dimensions may be different.

One such method is reversible jump MCMC [11]. Suppose there

are

models , and let the parameter vector for

model

be with dimension and support . The pa-

rameter space is regarded as a union of disjoint subspaces, i.e.,

, with for . In this case

(4)

剩余10页未读，继续阅读

changeerhao_love

粉丝: 6
资源: 35

粒子算法在目标跟踪参数估计与模型选择中的应用

MATLAB/Opencv实现IMM雷达多目标跟踪技术资料

利用辅助目标的动态背景目标跟踪策略

计算机视觉领域目标跟踪算法综述

目标跟踪相关资料论文总结

KCF.rar_KCF 目标跟踪_KCF目标跟踪_kcf precition_单目标跟踪_目标跟踪代码

PF.rar_PF 目标跟踪_PF 目标跟踪_目标跟踪_粒子滤波 跟踪_粒子滤波跟踪

PHD.rar_PHD tracking matlab_PHD 多目标跟踪_PHD多目标跟踪_phd 目标跟踪_多目标跟踪phd

目标跟踪,目标跟踪算法,matlab

目标跟踪系统的matlab 源程序包.zip_EKF_EKF 跟踪_discussjt2_matlab目标跟踪_目标跟踪EKF

粒子滤波英文资料用于多目标跟踪

最新资源

PF.rar_PF 目标跟踪_PF 目标跟踪_目标跟踪_粒子滤波跟踪_粒子滤波跟踪