编码理论基础：线性与卷积码详解

需积分: 15 3 下载量 133 浏览量 更新于2024-08-01 收藏 1.69MB PDF 举报
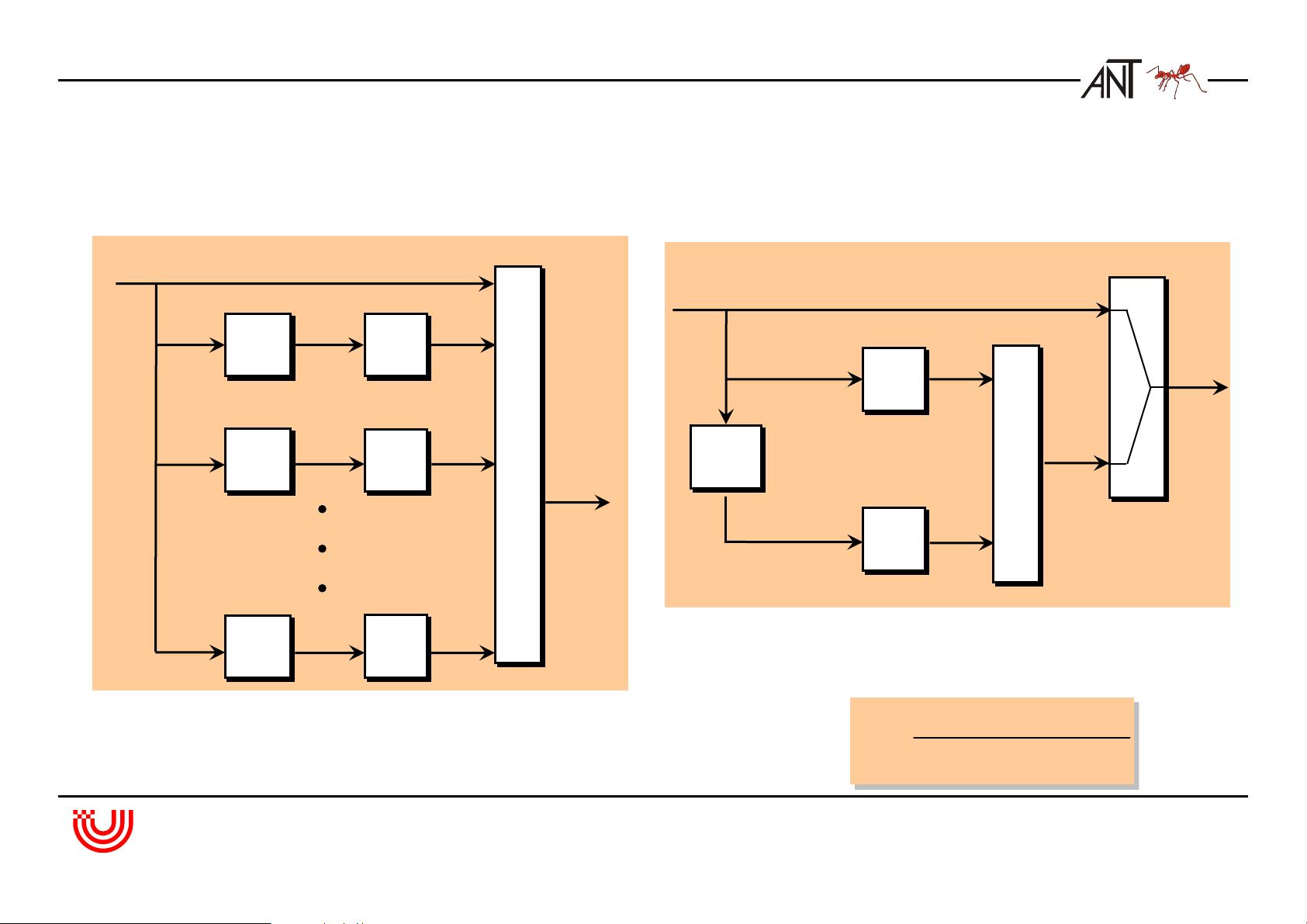
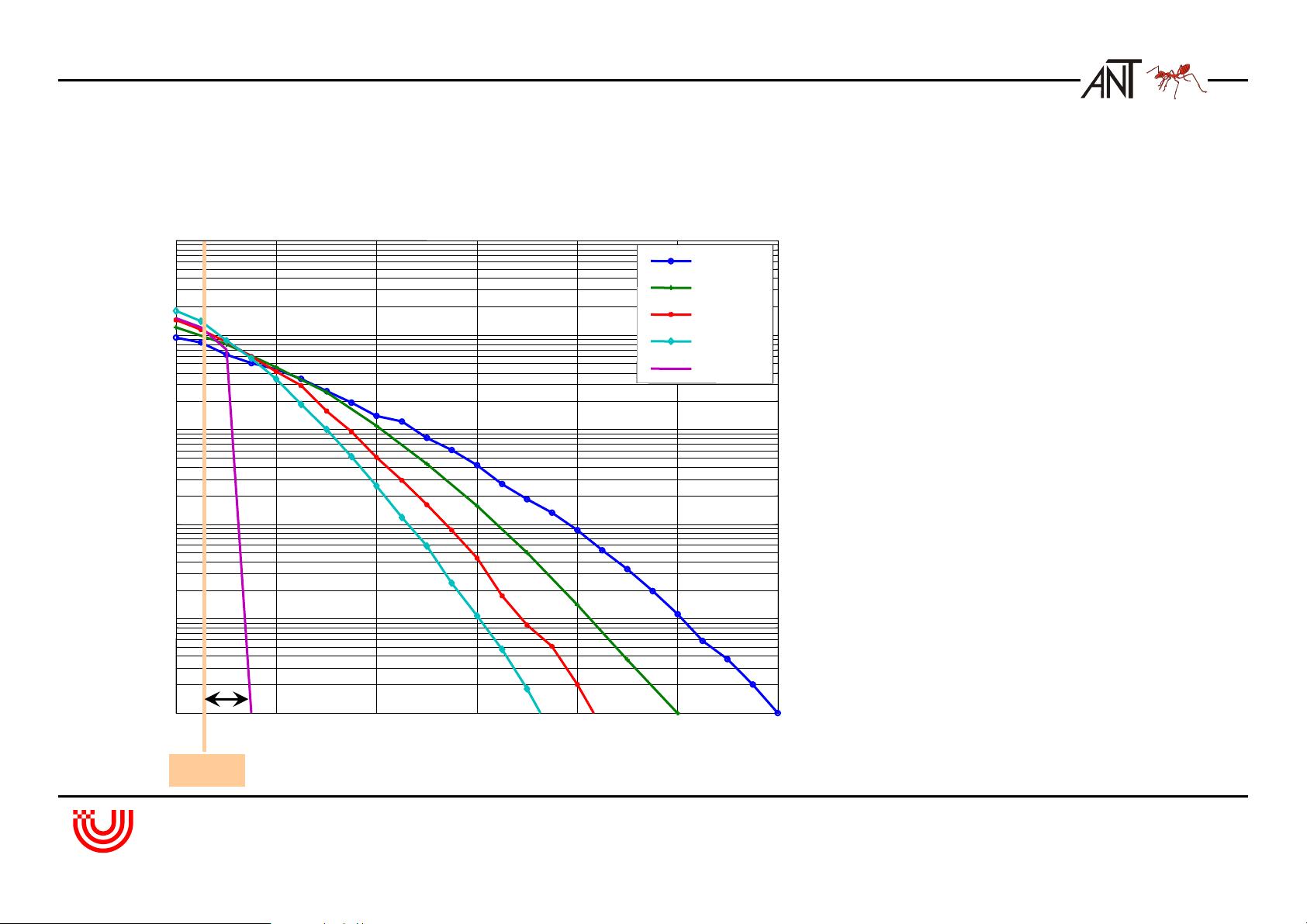
"《信道编码》课程概览" 这是一份针对信道编码的详细教学材料，由Dr.-Ing. Dirk Wübben教授主讲，隶属于不来梅大学的通信工程系。课程分为两部分：Channel Coding I 和 Channel Coding II。课程主要探讨信息论在数字通信系统中的核心应用，包括基本概念、概率理论、信息度量以及Shannon的信道容量理论。 Channel Coding I 的主要内容涵盖了： 1. 入门介绍：介绍了信道编码的基本原理和声明定义，以及数字通信系统的整体结构。 2. 信息论基础：讨论了概率的概念，以及如何衡量信息量，强调了Shannon通道容量理论在不同通信环境中的实际应用。 3. 线性块码：深入解析块码的性质，如错误率性能的边界，以及通过生成矩阵和校验矩阵表示的编码方法。此外，还重点讲解了循环码（如CRC码、Reed-Solomon码和BCH码）的特性和实现。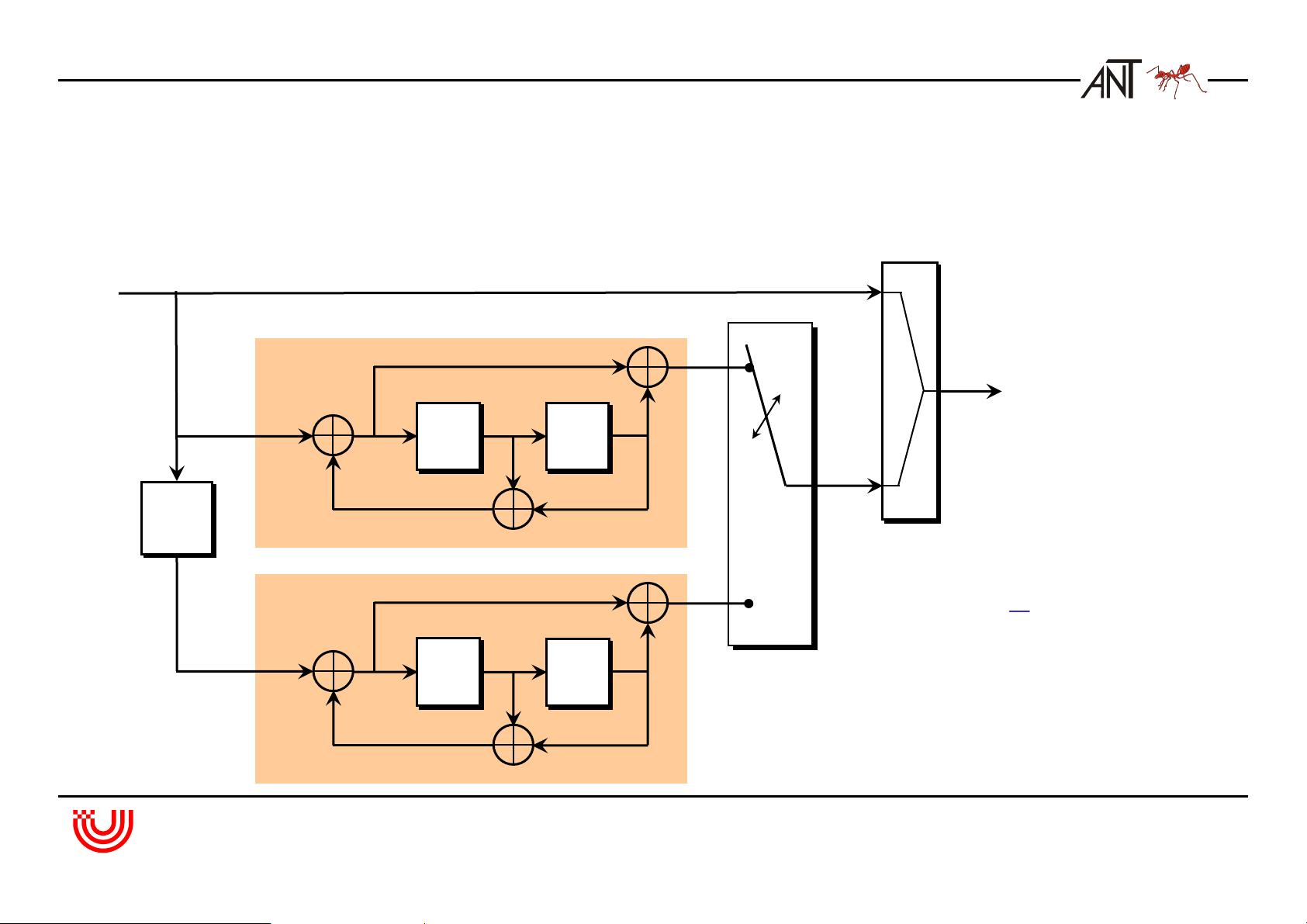 Channel Coding II 则进一步探讨了： 4. 卷积码：这部分介绍了卷积码的结构，包括其代数和图形表示方法。重点在于理解它们的距离特性，这些特性直接影响到编码的纠错能力。 课程安排上，每周二上午8:30至10:00在S1270进行讲座，而每周三下午14:00至16:00在N2420进行实践练习，具体的练习时间会在课堂上公布。课程的辅导老师是Carsten Bockelmann，他负责解答学生在学习过程中的疑问。 这份PDF文档是全英文的，对想要深入理解信道编码技术的学生来说是个宝贵资源。如果有需要，讲师表示愿意提供更多的相关资料。这门课程对于理解和设计高效、可靠的通信系统至关重要，是现代信息技术领域不可或缺的知识点。通过学习，学生将掌握如何对抗信号传输中的噪声干扰，提高数据传输的可靠性和有效性。"

TM SYNCHRONIZATION AND CHANNEL CODING

2015-03-26 上传
2011年CCSDS131.0-B-2版蓝皮书，为空间通信的遥测同步和信道编码提供新的标准。

Channel coding

2011-03-01 上传
根据提供的文档信息，我们可以深入探讨通道编码（Channel Coding）这一主题。通道编码是通信系统中的一个关键组成部分，它主要用于提高数据传输的可靠性。本篇内容将重点介绍文档中提到的关键概念和技术。 ### 一、...

Channel Coding Algorithms Theory and Applications

2017-06-12 上传
信道编码（Channel Coding）是一种在数据传输过程中用于提高数据可靠性的技术手段。它通过在原始数据上添加冗余信息来对抗信道噪声，从而确保接收端能够准确无误地恢复原始数据。该技术广泛应用于移动通信、卫星通信...

channel coding函数matlab

2023-07-25 上传
channel coding是一种用于提高通信系统可靠性的技术，其主要目的是在数据传输过程中引入冗余信息，以便在信道中出现噪声和误码时进行纠正。MATLAB是一种常用的科学计算和仿真软件，其中包括许多用于通信系统设计的...

Now apply channel coding to the transmitted data sequence. Use encode(msg,7,4,’hamming’), encode(msg,15,7,’bch’), and convenc, following the example listed in the help window (recall, in MATLAB type “help convenc” to obtain the help information for that command. For each of these codes, study how the code can reduce the BER and improve image quality for each SNR you studied above.

2023-06-11 上传
To apply channel coding to the transmitted data sequence, we can use the following codes: 1. Hamming Code (7,4): ```python import numpy as np from scipy import special from scipy import signal # ...

radio frequency channel coding made easy

2023-08-13 上传
无线电频道编码简化的方法有多种。其中一种常用的方法是使用纠错编码，例如海明码或卷积码。这些编码方法可以通过在数据流中引入冗余信息来提高信号的可靠性，使得在传输过程中出现的误差可以被检测和纠正。...

A = imread('krabi1.bmp','BMP'); %read in the image A_shrunk = imresize(A,0.2); % we’ll reduce the resolution, as otherwise the file size is too large imshow(A_shrunk) % displays the shrunken image Bs = reshape(A_shrunk,[388*518*3,1,1]); % resizes this image from a pixel array of three colours to a one-dimensional data stream C = de2bi(double(Bs)); % converts these values to binary representation % You can then resize this array to a linear, one-dimensional array. % this data stream C is then what you can communicate over your channel. % recover the image from the binary sequence BS_rec = uint8(bi2de(C)); % convert bits to pixel values. A_rec = reshape(BS_rec,[388,518,3]); % reshape back to a coloured pixel array. imshow(A_rec) % display the recovered image. Explore the pskmod and pskdemod commands in MATLAB. Use these to modulate and demodulate the binary sequence into a binary PSK signal. (Hint: the command should be something like D = pskmod(C,2). Display a part of this signal, and explain carefully how we have represented this signal in MATLAB, and how it differs from the analysis we performed in Part A. Transmit this signal through an AWGN channel using the awgn() function for a range of signal to noise ratios. Demodulate and comment on the effect of the noise on the image. A suitable range of signal to noise ratios is –0.5dB to 5 dB. The bit error rate refers to the fraction of bits that are received in error. This can also be interpreted as the probability that a bit is received in error. Calculate the bit error rate (BER) for the signal to noise ratios you used above. Comment on the correlation between BER and perceptual image quality. Now apply channel coding to the transmitted data sequence. Use encode(msg,7,4,’hamming’), encode(msg,15,7,’bch’), and convenc, following the example listed in the help window (recall, in MATLAB type “help convenc” to obtain the help information for that command. For each of these codes, study how the code can reduce the BER and improve image quality for each SNR you studied above.

2023-06-10 上传
这是一个关于数字图像处理和通信的问题，需要一些MATLAB知识。下面是对问题的回答： 1. 读入并压缩图像 首先，使用`imread`函数读入一张图片，并使用`imresize`函数将图片压缩到原来的20%大小： ...

无线信号传输包含信道编码和什么

2023-07-12 上传
1. 信道编码（Channel Coding）：在无线信道传输中，由于信道的噪声、干扰和衰落等因素，传输过程中可能会引入错误。为了提高传输的可靠性，信道编码被用于在发送端对数据进行编码，并在接收端进行解码。信道编码...

香农信息论中的级别都是哪些

2023-07-14 上传
2. 第二级别：信道编码（Channel Coding）- 在信道传输中引入冗余信息，以增强对抗噪声和失真的能力，提高传输的可靠性。 3. 第三级别：通信感知一体化（Communication Perception Integration）- 将通信和感知两个...

deepjscc代码

2023-08-13 上传
- *1* *3* [Deep Joint Source Channel Coding for Wireless Image Transmission with OFDM 论文总结](https://blog.csdn.net/qq_25355771/article/details/122309674)[target="_blank" data-report-click={"spm":...
timpanzer
  • 粉丝: 0
  • 资源: 3
上传资源 快速赚钱

最新资源