Python机器学习：构建多层神经网络与tanh激活函数

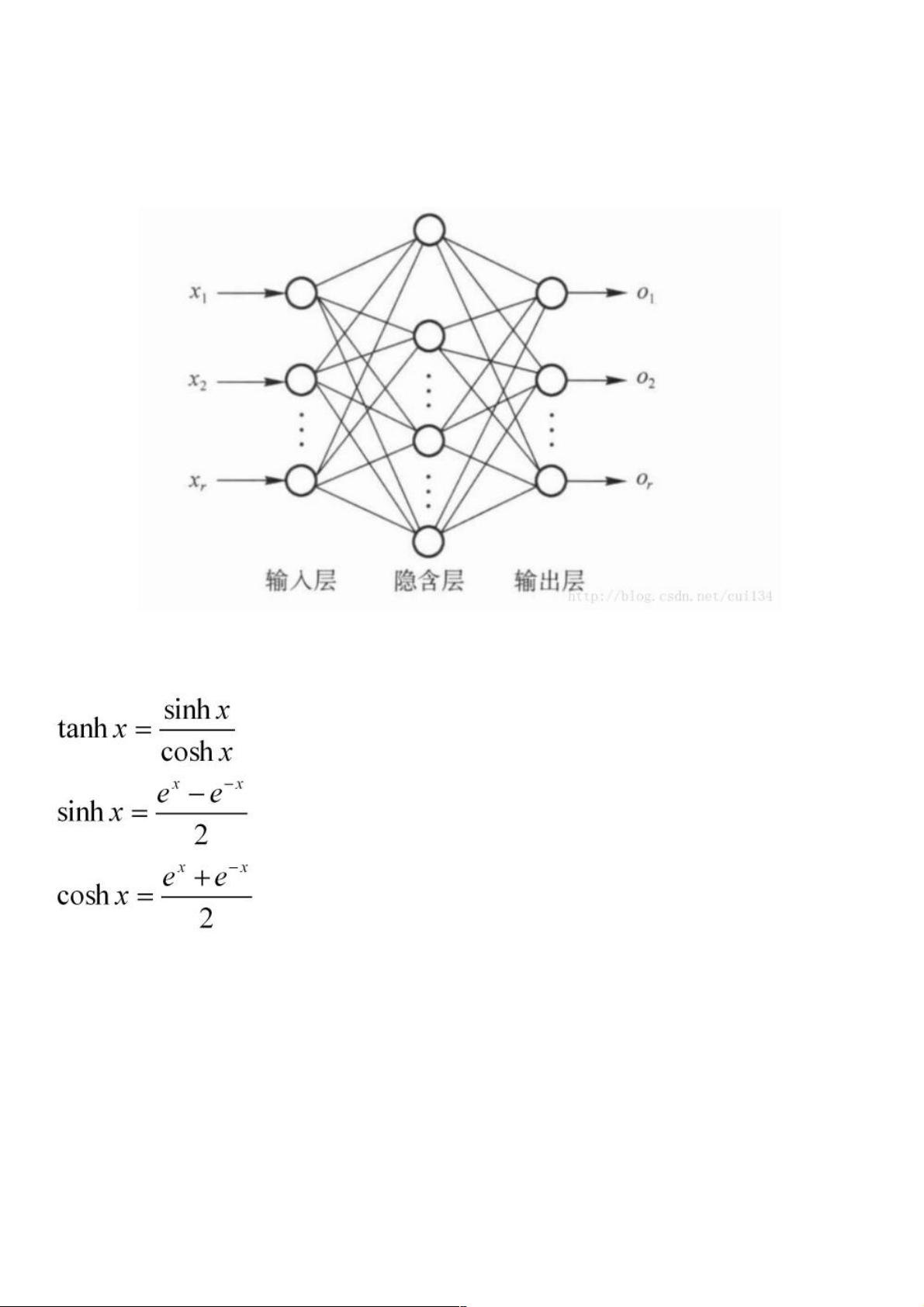
"这篇教程是关于Python机器学习中的神经网络的第二部分，主要讨论了多层感知器结构以及tanh激活函数在神经网络中的应用。文章通过实例代码展示了如何使用Python实现一个包含多个隐藏层的神经网络，并用二维数据进行训练。" 在Python机器学习中，神经网络是一种强大的工具，尤其在处理复杂数据分类和回归问题时。在第一篇教程的基础上，本文深入到神经网络的多层结构，以克服Rosenblatt感知器对于非线性分类的局限性。多层感知器（Multilayer Perceptron, MLP）引入了隐藏层，这些隐藏层配合激活函数可以创建复杂的非线性决策边界，从而解决线性不可分的问题。 激活函数是神经网络中的关键组成部分，它将神经元的输入转化为输出，赋予网络非线性表达能力。在本文中，作者选择了tanh（双曲正切）函数作为激活函数，其公式为： `tanh(z) = (e^z - e^(-z)) / (e^z + e^(-z))` tanh函数的形状介于-1和1之间，这使得它的输出更便于优化。相比硬限幅函数，tanh函数在所有点都可导，有利于反向传播算法进行权重更新。 神经网络的权重更新通常使用梯度下降法，局部梯度计算是这个过程的一部分。对于隐藏层神经元，局部梯度分为两种情况：神经元不在隐藏层和神经元在隐藏层。权重的更新规则基于这些局部梯度和学习率，以减小损失函数（如均方误差MSE）。 在提供的Python代码示例中，作者构建了一个包含多个隐藏层的神经网络模型，每个隐藏层有8个节点，共7个隐藏层，最后是一个包含2个单元的输出层。训练数据是二维的，用于可视化结果。通过迭代和设定误差阈值，神经网络会逐渐调整权重，以达到最佳的分类性能。 值得注意的是，代码中还包含了sigmoid函数的定义，尽管本文主要使用了tanh函数，sigmoid函数在神经网络中也是一种常见的激活函数，特别是在输出层用于二分类问题。 本教程通过理论解释和实际代码演示了如何在Python中构建和训练一个多层神经网络，这对于初学者理解神经网络的工作原理和实践操作非常有帮助。此外，对于想要深入研究机器学习和神经网络的读者，理解激活函数的作用、权重更新的机制以及如何设计网络结构是非常重要的。