Fisher线性判别：Iris和Sonar数据集的高效分类

Fisher线性判别是一种经典的统计学方法，特别适用于线性可分的模式识别任务，它在机器学习领域广泛应用。该方法源于R.A. Fisher的理论，旨在通过最大化类别间的方差和最小化类内的方差，来构建一个最优的超平面，从而实现数据的高效分类。 在处理Iris和Sonar数据集时，Fisher线性判别首先通过以下步骤进行操作： 1. 数据预处理：选择UCI数据集，这是一个常用的数据集库，通常包含来自现实世界的、随机分布且无明显变化趋势的数据。为了评估训练集大小对结果的影响，数据被划分为训练集和测试集，采用随机或均匀采样策略。 2. 分类任务：对于Sonar数据集，它是一个二分类问题，包含207个样本，每个样本有60个特征。若Fisher线性判别在此数据上表现良好，说明其在高维数据中的分类能力显著。为了验证，先计算两类数据的中心（均值）和离散度，然后构造优化函数，基于类内离散度最小和类间离散度最大原则，简化并求解这个函数。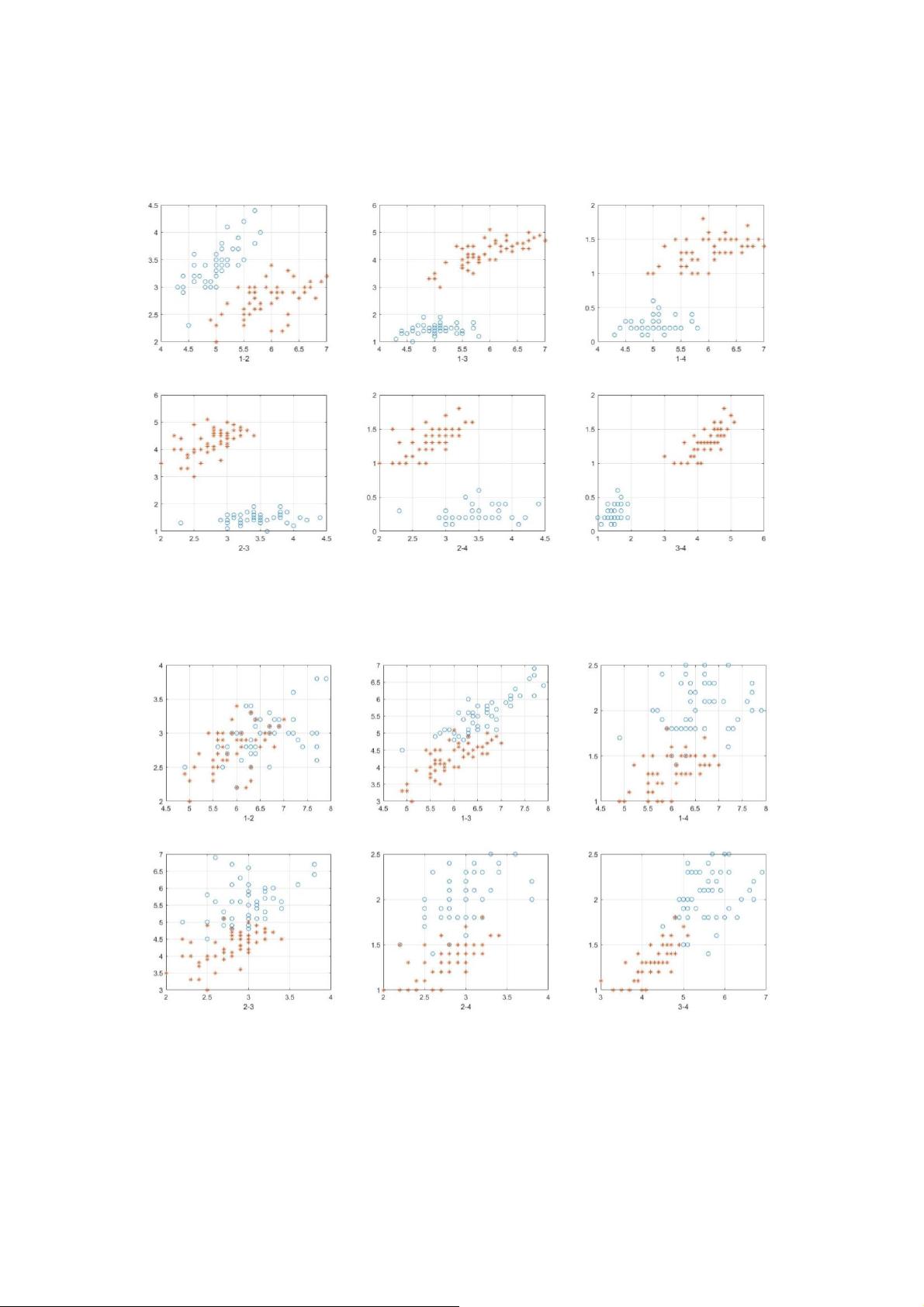 3. 扩展至多分类：对于Iris数据集，它是三分类问题，包含150个样本，每个样本有4个特征。通过将三分类问题分解为多个二分类任务，如将数据分为第一类与第二类、第一类与第三类以及第二类与第三类，然后合并分类结果，以此检验Fisher线性判别在多分类场景中的适用性。 4. 结果评估：对Sonar数据集进行二分类，达到了80%的分类准确率，显示出该方法的有效性。而对于Iris数据集的三分类任务，尽管具体百分比未给出，但其分类性能同样重要，因为它表明Fisher线性判别不仅适用于二分类，也适用于更高维度的线性可分问题。 总结来说，Fisher线性判别是一种强大的工具，它利用统计学原理有效地解决线性可分的数据分类问题，通过优化离散度来创建最优决策边界。无论是二分类还是多分类任务，只要数据满足线性可分条件，Fisher线性判别都能提供出色的分类性能，尤其适用于特征较多的高维数据集。