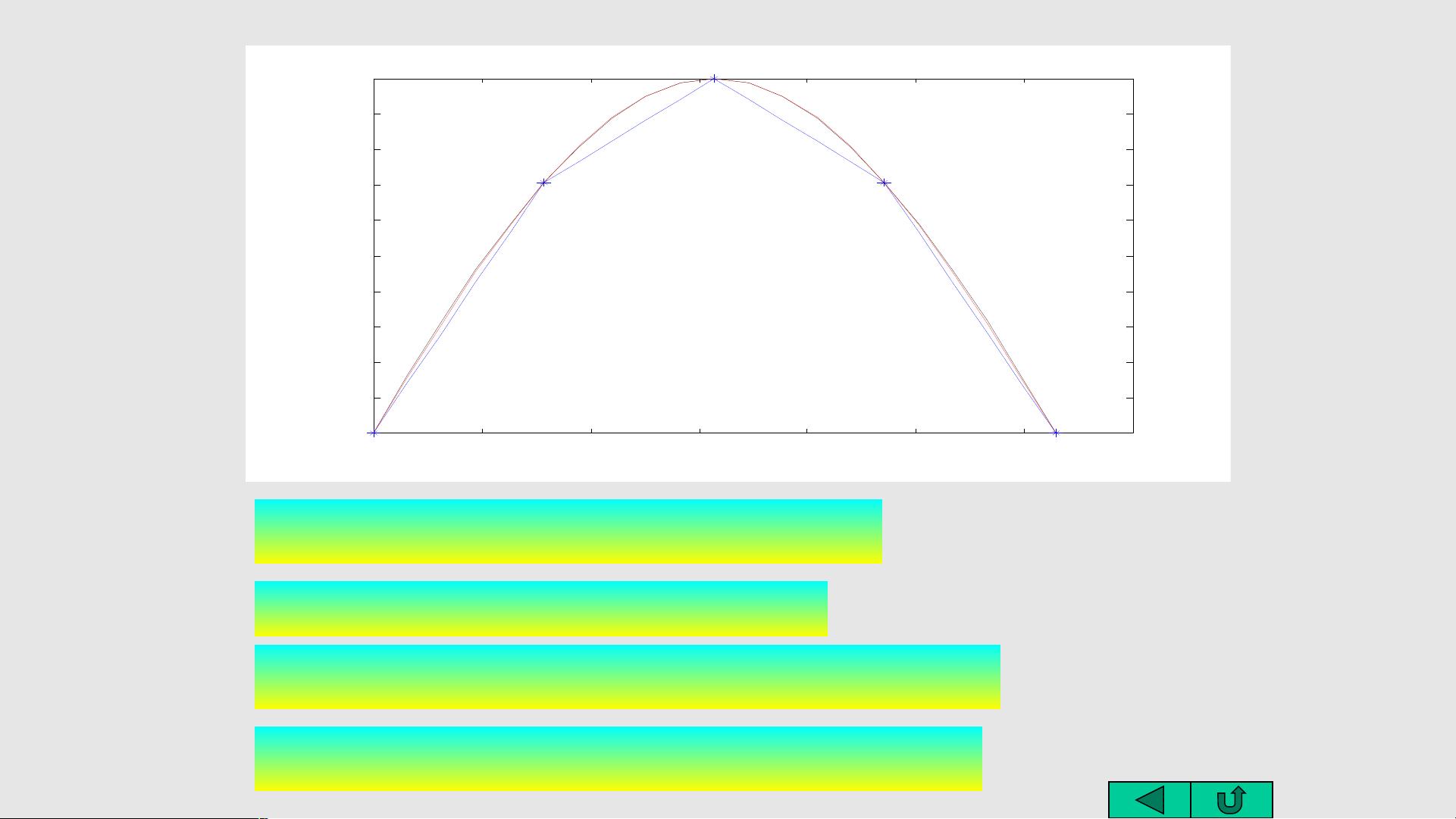
"高效的拉格朗日插值方法及其应用"

本章主要介绍插值法的基本概念和多项式插值的基础理论，以及几种常用的插值方法，包括拉格朗日插值、分段线性插值、牛顿插值、Hermite插值和三次样条插值。在实际应用中，我们常常需要通过离散数据点来逼近一个复杂的函数。插值法作为一种简单有效的逼近方法，可以通过少量的已知数据点来构建一个近似函数，从而表示原始函数。其中，拉格朗日插值多项式、差商与牛顿插值公式、差分与等距节点插值公式、分段低次插值和三次样条插值等方法都是常用的插值技术。通过这些插值方法，我们可以有效地逼近原始函数，进而进行更深入的数值计算和分析。在实际应用中，插值法在数据处理、图像处理、物理建模等领域都具有重要的应用价值，能够帮助我们处理和分析复杂函数的数据，从而更好地理解和利用现实世界中的各种信息。拉格朗日插值法作为其中一种经典方法，通过构建一个多项式函数来逼近原始函数，从而实现对原函数的有效近似。在拉格朗日插值公式中，我们需要通过已知的数据点来构建一个多项式函数，从而表示原始函数。通过掌握插值法的基本概念和应用技巧，我们可以更好地理解和利用数值计算方法，从而在实际问题中应用插值技术，提高工作效率和求解准确度。在数值计算和科学计算领域，插值法是一种重要的数值分析技术，能够帮助我们处理和分析复杂的函数关系，解决实际问题，推动科学研究和技术发展。通过学习插值法的原理和方法，我们可以更好地理解数值计算的基础知识，从而更好地应用数值方法解决实际问题。拉格朗日插值法作为其中一种经典的插值技术，在科学计算和工程应用中具有广泛的应用价值，能够帮助我们有效地处理和分析复杂的函数关系，解决实际问题，促进科学研究和技术创新。在插值法的应用过程中，我们需要根据具体问题选择合适的插值方法，结合实际情况进行适当的调整和优化，以实现对原函数的准确近似。通过插值法的应用，我们可以更加全面地理解和分析数值计算方法，加深对数值计算理论的理解，从而更好地应用数值方法解决实际问题。通过本章的介绍和学习，我们可以更好地掌握插值法的基本原理和方法，进而运用插值技术解决实际问题，促进科学研究和技术创新的发展。