有限差分算法(FDTD)详解：从麦克斯韦方程到边界条件

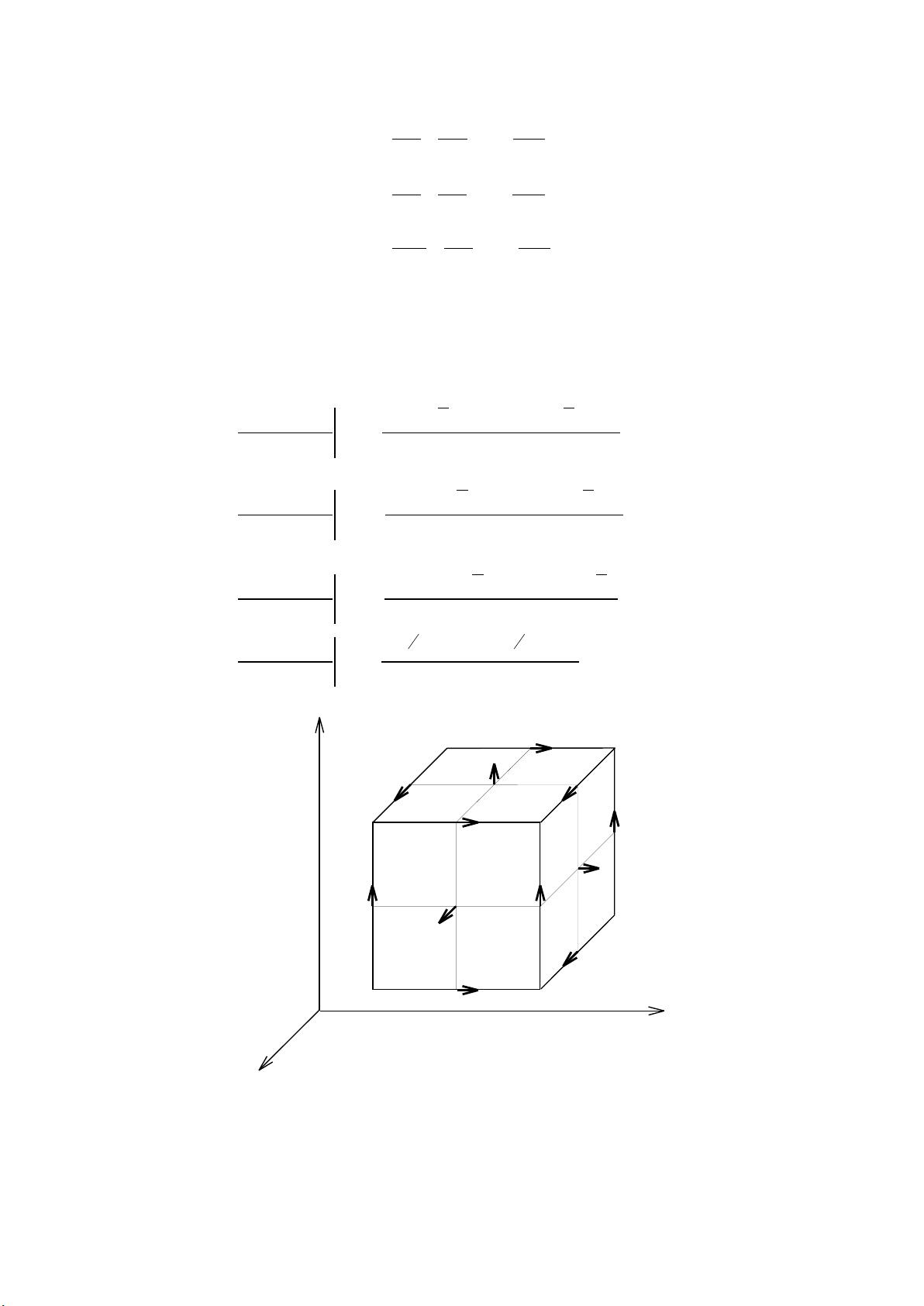
有限差分算法(Finite Difference Time Domain, FDTD)是一种广泛应用于电磁场模拟、光学、电子学以及信号处理等领域的重要数值方法。FDTD起源于20世纪60年代，它将麦克斯韦方程组通过差分方式近似求解，实现了对电磁波在空间和时间上的离散化处理，使得复杂问题能够在计算机上进行仿真计算。 FDTD的核心思想是将连续的电磁场理论分解为空间网格和时间步进，通过Yee网格结构（将电场和磁场分布在网格节点上，便于同时考虑它们之间的相互作用）来实现。算法主要包括以下几个关键部分： 1. **麦克斯韦方程与Yee元胞**：FDTD的基础是麦克斯韦方程，特别是Maxwell-Yee公式，它们在直角坐标系下被转化为一维、二维和三维的形式。Yee元胞结构有助于简化计算并保持物理一致性。 2. **时间离散与空间离散**：算法的关键是时间步进法，通常采用欧拉或亚欧拉方法进行时间离散，而Courant-Friedrichs-Lewy (CFL)条件确保了时间步长的选择以保证数值稳定性。空间离散则涉及到不同的差分格式，如中心差分法，可以减小数值色散误差。 3. **吸收边界条件**：为了减少波的反射，FDTD引入了各种吸收边界条件，如Mur吸收边界条件，包括一阶和二阶近似，以及Engquist-Majda边界条件，它们用于模拟无限空间或边界处的电磁波行为。 4. **完全匹配层 (Perfectly Matched Layer, PML)**：PML是一种特殊的技术，通过引入人工吸收边界，使外部区域的波能量逐渐衰减到零，有效地模拟无限大域。Berenger的PML采用指数差分，提供了一种高效且低反射的边界处理方式。 5. **各向异性介质处理**：对于非均匀或各向异性的介质，FDTD需要适应性地调整电导率和磁导率的差分表达，如二维和一维 Mur边界条件，以及针对不同几何结构（如棱边、角顶）的特殊处理。 FDTD算法的学习者会从麦克斯韦方程的基本原理入手，逐渐掌握时空离散策略、数值稳定性分析、边界条件设计以及复杂介质的处理技巧。通过深入理解和实践这些内容，他们能够熟练运用FDTD方法解决实际的电磁场问题。此外，每章末尾的复习思考题和参考文献为深入研究提供了丰富的扩展资源。