有限元方法解线性代数方程组:高斯消去与迭代法
需积分: 10 175 浏览量
更新于2024-08-02
收藏 761KB PDF 举报
"有限单元法_王勖成课件7"
有限单元法是工程和科学计算中解决偏微分方程的一种数值方法,通常用于结构力学、流体力学等领域。在这一课件中,主要讨论了线性代数方程组的解法,这是有限单元法中的核心部分。线性代数方程组常常来源于有限元分析中的刚度矩阵和载荷向量。
1. 高斯消去法和三角分解法:这两种方法是求解线性代数方程组的基本算法。高斯消去法通过一系列行变换将系数矩阵转化为上三角矩阵,然后通过回代求解。三角分解法,也称为LU分解,是将系数矩阵分解为一个下三角矩阵L和一个上三角矩阵U,然后分别求解两个三角形系统的线性组合。
2. 二维等带宽存储和一维变带宽存储:这些是针对稀疏矩阵的存储策略。二维等带宽存储适用于带状矩阵,即非零元素在矩阵主对角线两侧具有固定宽度。一维变带宽存储则更灵活,适合非零元素分布不规则的情况。两者各有优缺点,等带宽存储便于访问但空间利用率低,变带宽存储节省空间但访问可能复杂。
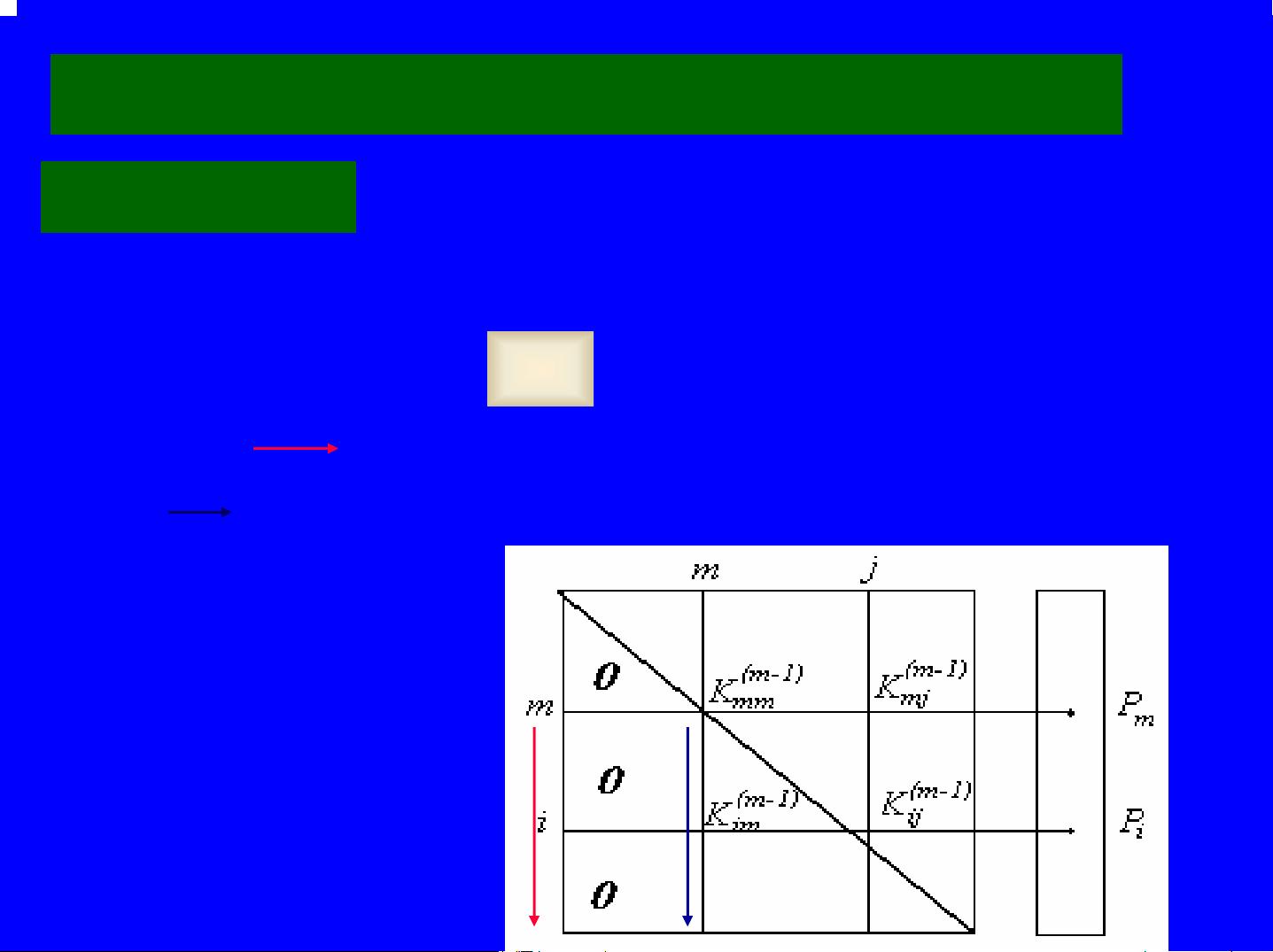
3. 分块解法:当大型线性系统太大无法一次性处理时,可以将其划分为较小的子问题来求解。这种方法减少了内存需求和计算复杂性,尤其适用于结构或物理问题中存在自然分块的情况。
4. 迭代解法:包括超松弛迭代法、梯度法、共轭梯度法和预条件共轭梯度法。这些方法适合于大型稀疏矩阵,通过迭代逐渐接近解,通常比直接解法更节省内存,但可能需要更多的计算步数。超松弛因子影响迭代的收敛速度,对对角优势较弱的矩阵,较大的超松弛因子可能有助于收敛。
5. 节省内存和计算效率:迭代解法允许在每一步迭代中只更新部分变量,因此在编程时可以利用这种局部更新的特点,有效利用内存并减少计算开销。
6. 预条件共轭梯度法:预条件器是为了加速共轭梯度法的收敛,选择适当的预条件矩阵能够显著改善计算效率,尤其是在处理大型复杂问题时。
本课件详细阐述了这些解法的原理、步骤和应用场景,对于理解和应用有限单元法解决实际问题至关重要。同时,通过复习题的形式,强化了对这些概念的理解和应用能力。
2010-01-17 上传
2010-01-17 上传
2010-01-17 上传
2010-01-17 上传
2010-01-17 上传
2010-01-17 上传
langjin
- 粉丝: 0
- 资源: 22
最新资源
- WordPress作为新闻管理面板的实现指南
- NPC_Generator:使用Ruby打造的游戏角色生成器
- MATLAB实现变邻域搜索算法源码解析
- 探索C++并行编程:使用INTEL TBB的项目实践
- 玫枫跟打器:网页版五笔打字工具,提升macOS打字效率
- 萨尔塔·阿萨尔·希塔斯:SATINDER项目解析
- 掌握变邻域搜索算法:MATLAB代码实践
- saaraansh: 简化法律文档,打破语言障碍的智能应用
- 探索牛角交友盲盒系统:PHP开源交友平台的新选择
- 探索Nullfactory-SSRSExtensions: 强化SQL Server报告服务
- Lotide:一套JavaScript实用工具库的深度解析
- 利用Aurelia 2脚手架搭建新项目的快速指南
- 变邻域搜索算法Matlab实现教程
- 实战指南:构建高效ES+Redis+MySQL架构解决方案
- GitHub Pages入门模板快速启动指南
- NeonClock遗产版:包名更迭与应用更新