逻辑代数与VerilogHDL基础教程

“数字电路：2 .逻辑代数与硬件描述语言基础.pdf” 本文将深入探讨逻辑代数及其在数字电路中的应用，同时介绍硬件描述语言Verilog HDL的基础知识。逻辑代数，又称为布尔代数，是数字系统设计的核心理论，由数学家George Boole在1849年创立。它提供了描述和简化数字逻辑电路的方法。 **2.1 逻辑代数** 逻辑代数主要包含一系列基本定律、恒等式和规则，这些规则对于理解和简化逻辑电路至关重要。以下是一些关键概念： 1. **基本定律和恒等式**： - **0、1律**：任何量与1相乘等于其本身（A·1=A），任何量与0相乘等于0（A·0=0）。 - **交换律**：加法和乘法操作具有交换性（A+B=B+A，A·B=B·A）。 - **结合律**：加法和乘法操作具有结合性（A+B+C=(A+B)+C，A·B·C=(A·B)·C）。 - **分配律**：乘法操作对加法有分配性（A+BC=(A+B)(A+C)，A(B+C)=AB+AC）。 - **互补律**：一个量与其非操作（NOT）结果相加等于1（A+A=1），相乘等于0（A·A=0）。 - **重叠律**：重复项可以被吸收（A+A=A，A·A=A）。 - **反演律**：AND和OR操作可以通过非操作转换（AB=A+B，A+B=A·B）。 2. **逻辑函数的变换及代数化简法**： - **卡诺图化简法**：通过绘制卡诺图，可以直观地找到最小项，从而简化逻辑函数。例如，AB+AC+BC可以用AB+AC来表示，因为AB+AC+BC=AB+(A+C)B=AB+AB=AB。 3. **常用公式**： - 互补律的推论：AB+AB=A（De Morgan's定律的特例）。 - **德摩根定律**：非加法等于乘法的非，非乘法等于加法的非（A+BC=(A'+B')(A'+C')，A·B=A'·B'）。 - **异或（XOR）**：异或运算符“⊕”表示不一致时为1，一致时为0（如A⊕A=0，A⊕B=B⊕A，A⊕0=A，A⊕1=¬A）。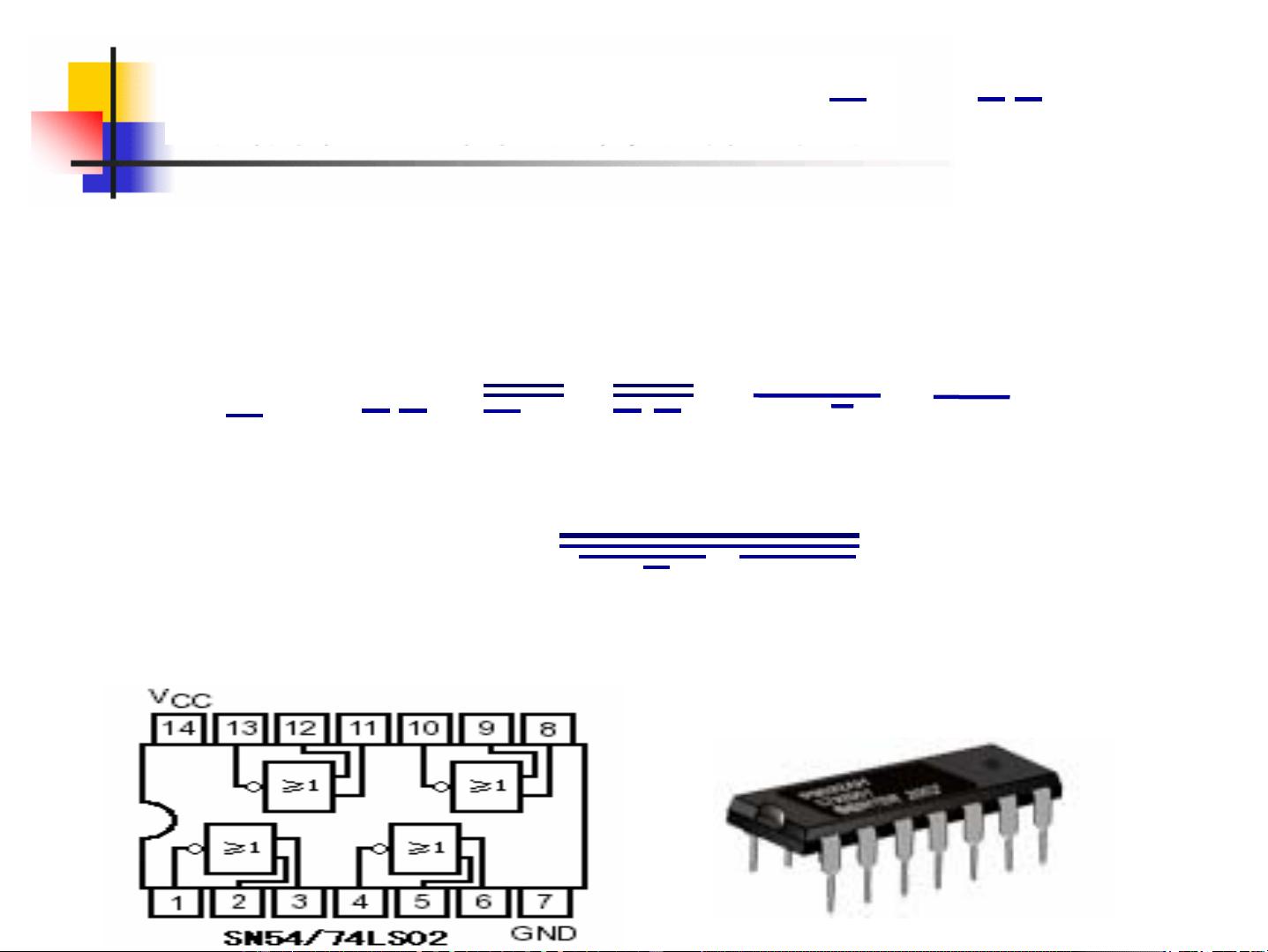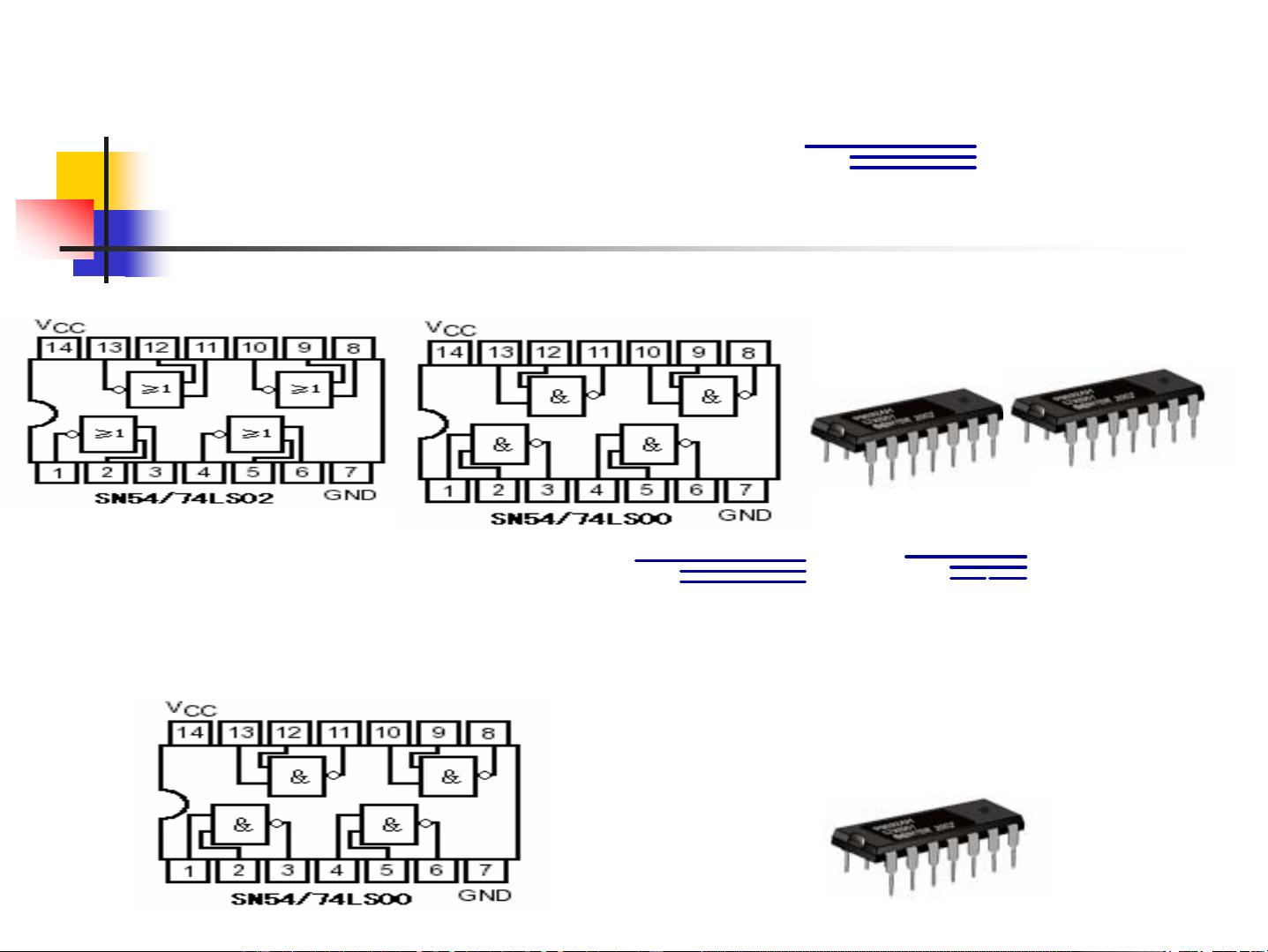 - **与非（NAND）和或非（NOR）**：A·B=A'B'，A+B=A'B'，是所有其他逻辑运算的基础。 **2.3 Verilog HDL基础** Verilog HDL是一种硬件描述语言，用于设计和验证数字系统。它允许工程师用接近于自然语言的方式来描述电路行为。理解Verilog的关键概念包括： 1. **数据类型**：Verilog提供了位（bit）、字节（byte）、短整型（shortint）、整型（int）、长整型（longint）等多种数据类型。 2. **结构体**：可以定义模块（module），模块是Verilog设计的基本单元，包含了输入、输出、内部变量以及行为描述。 3. **赋值操作**：使用`=`进行连续赋值，`=<=`进行非阻塞赋值，适用于描述并行操作。 4. **控制结构**：包括顺序控制（如always块内的if-else，for，while循环）和并发控制（如always@*块）。 5. **综合与仿真**：Verilog代码可以被综合成硬件描述，也可以用于模拟和验证设计的功能正确性。 学习这些基础知识，能够帮助理解和设计数字电路，以及使用Verilog HDL进行有效的硬件描述。通过结合逻辑代数的规则和Verilog HDL的编程，可以创建复杂而高效的数字系统。