最优化方法：目标、方案与限制条件详解

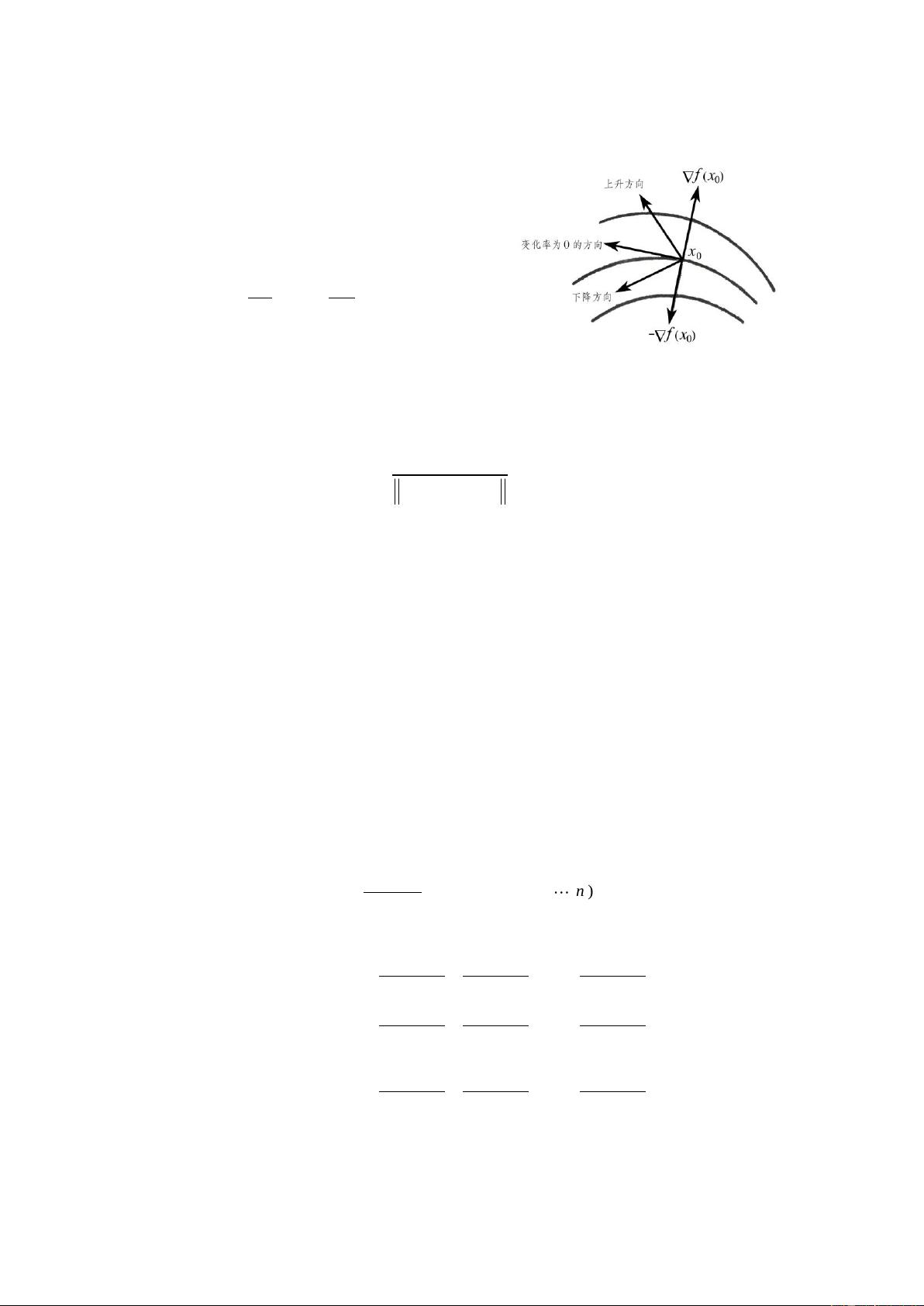
最优化方法及其应用是一门研究如何在各种可能的解决方案中选择最佳策略以实现最优目标的学科。它涉及到数学建模和分析，广泛应用于工程、经济、管理等领域。本资源的核心内容包括以下几个方面： 1. 定义与概念：最优化问题的基本定义指出，人们在决策时倾向于寻求以最小成本或资源消耗获取最大效益。这涉及在给定条件下的方案选择，其中目标是方案的函数，且可能存在一定的限制条件。 2. 要素构成：最优化问题通常包含三个关键元素：目标（期望达到的结果），方案（可供选择的方法或策略），以及限制条件（约束条件，如预算、时间或技术限制）。目标函数必须是方案变量的函数，以确保问题的数学化处理。 3. 分类：根据问题的时间依赖性，最优化分为静态和动态两种类型。静态问题不考虑时间因素，如上面提到的制作水槽容积最大化的例子，而动态优化则涉及随时间变化的情况。 4. 数学模型示例：书中举例了函数极值问题，如正方形铁板剪切成水槽和侧面积固定情况下长方体体积最大化的问题。通过求解这些数学模型，可以找到最优解。在正方形水槽的例子中，通过计算驻点并检验其性质，确定了剪切边长为6a的正方形能得到最大容积。 5. 方法工具：解决这类问题常用到的数学工具包括拉格朗日乘数法，如在长方体体积最大化问题中，通过引入额外的拉格朗日乘数来处理约束条件。 总结来说，最优化方法是一门实用的决策分析技术，通过构建和求解数学模型，帮助人们在复杂决策环境中找到最优解决方案。理解和掌握这一领域的知识对于工程师、经济学家和决策者来说具有重要意义。