C语言实现二叉树应用：建立、遍历、操作节点

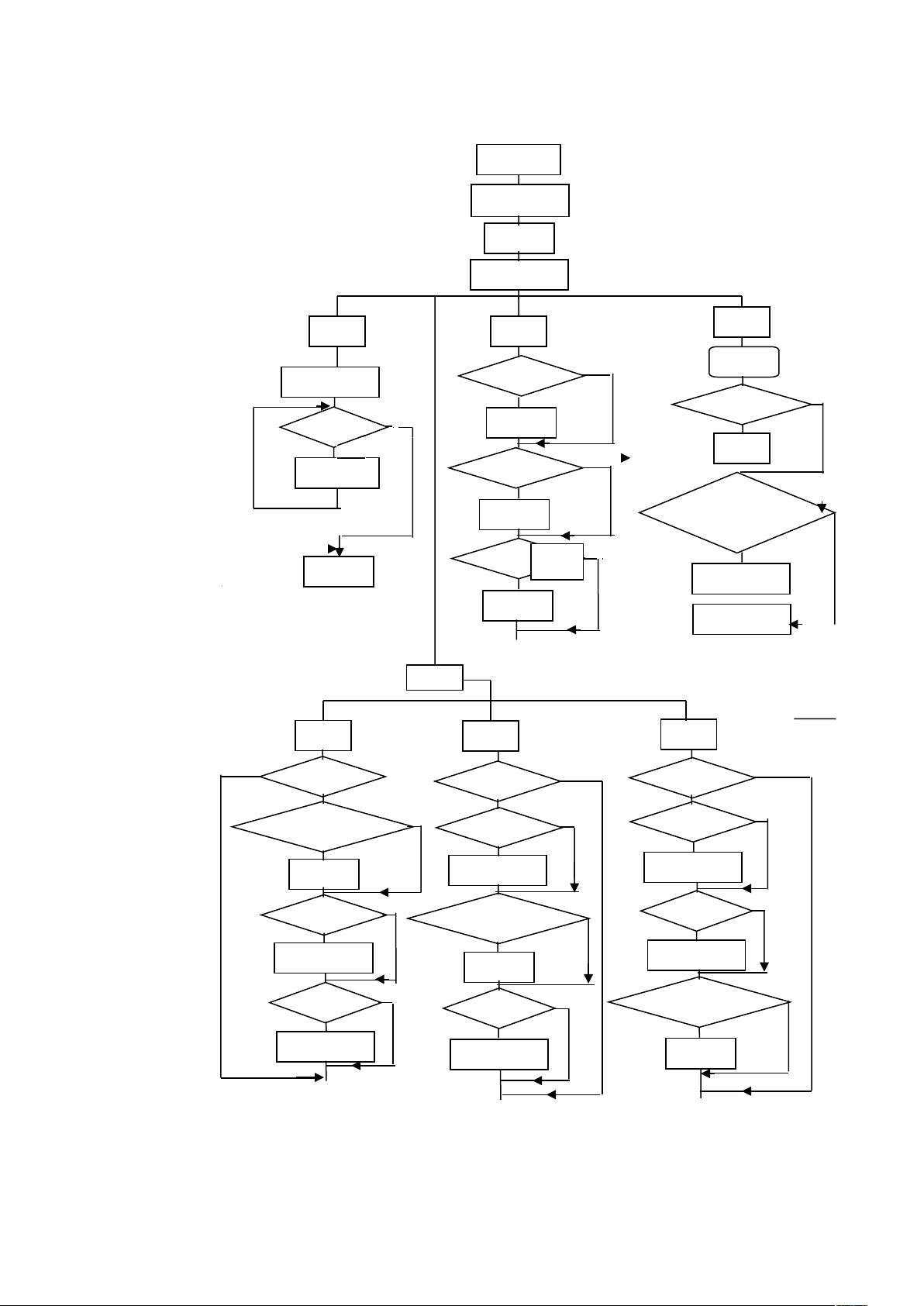
"二叉树的应用，涉及二叉树的创建、遍历、计算深度、查找特定节点、计算叶节点数量以及添加和删除节点的操作。这份报告是针对C语言与数据结构实习的一个项目，旨在巩固和提升学生的理论知识和编程技能，特别是在C语言和数据结构应用方面。" 在计算机科学中，二叉树是一种基础且重要的数据结构，它由节点组成，每个节点最多有两个子节点，通常分为左子节点和右子节点。在二叉树的应用中，以下是一些关键概念和操作： 1. **二叉树的建立**：创建二叉树通常通过一系列的插入操作完成，可以使用递归或非递归方法。在插入过程中，根据新元素与现有节点的相对大小关系来决定其位置。 2. **遍历**：二叉树有三种主要遍历方式：前序遍历（根-左-右）、中序遍历（左-根-右）和后序遍历（左-右-根）。遍历主要用于访问树中的所有节点，按照特定顺序。 - **前序遍历**：首先访问根节点，然后遍历左子树，最后遍历右子树。 - **中序遍历**：首先遍历左子树，然后访问根节点，最后遍历右子树，常用于实现二叉搜索树的排序。 - **后序遍历**：首先遍历左子树，然后遍历右子树，最后访问根节点，常用于计算表达式树等。 3. **求二叉树的深度**：深度是指从根节点到最远叶节点的最长路径上的边数。可以通过递归方法计算，对于非空树，深度是左子树和右子树深度中较大的那个加1。 4. **查找指定结点**：在二叉搜索树中，可以通过比较节点值来快速定位目标节点。在非有序二叉树中，可能需要自顶向下遍历整个树。 5. **求叶子结点的数目**：叶子节点是没有子节点的节点。可以通过递归遍历来计算，每遇到一个没有子节点的节点，计数器加1。 6. **添加结点**：向已有的二叉树添加新节点，需要找到合适的位置。对于二叉搜索树，新节点会根据其值被插入到正确的位置。 7. **删除结点**：删除节点操作较复杂，要考虑被删除节点是否有子节点。无子节点的删除直接移除，有子节点的需要考虑替换策略，如最小右子节点或最大左子节点替换。 在实际编程中，为了实现这些操作，通常定义一个`TreeNode`结构体，包含节点值、左子节点指针和右子节点指针。此外，还需要编写相应的函数来执行上述操作，例如`creatTree()`用于创建树，`PreOrderTraverse()`、`InOrderTraverse()`和`PostOrderTraverse()`分别用于前序、中序和后序遍历，`Count1()`和`Count2()`用于计算树的高度，以及查找和删除节点的函数。 实习报告的编写要求学生不仅实现这些功能，还要能够清晰地阐述设计思路，编写详细的文档，包括设计说明、代码实现、测试结果和总结，以展示对C语言和数据结构知识的深入理解和应用能力。