TMS320LF2407 DSP中的FFT算法实现与应用

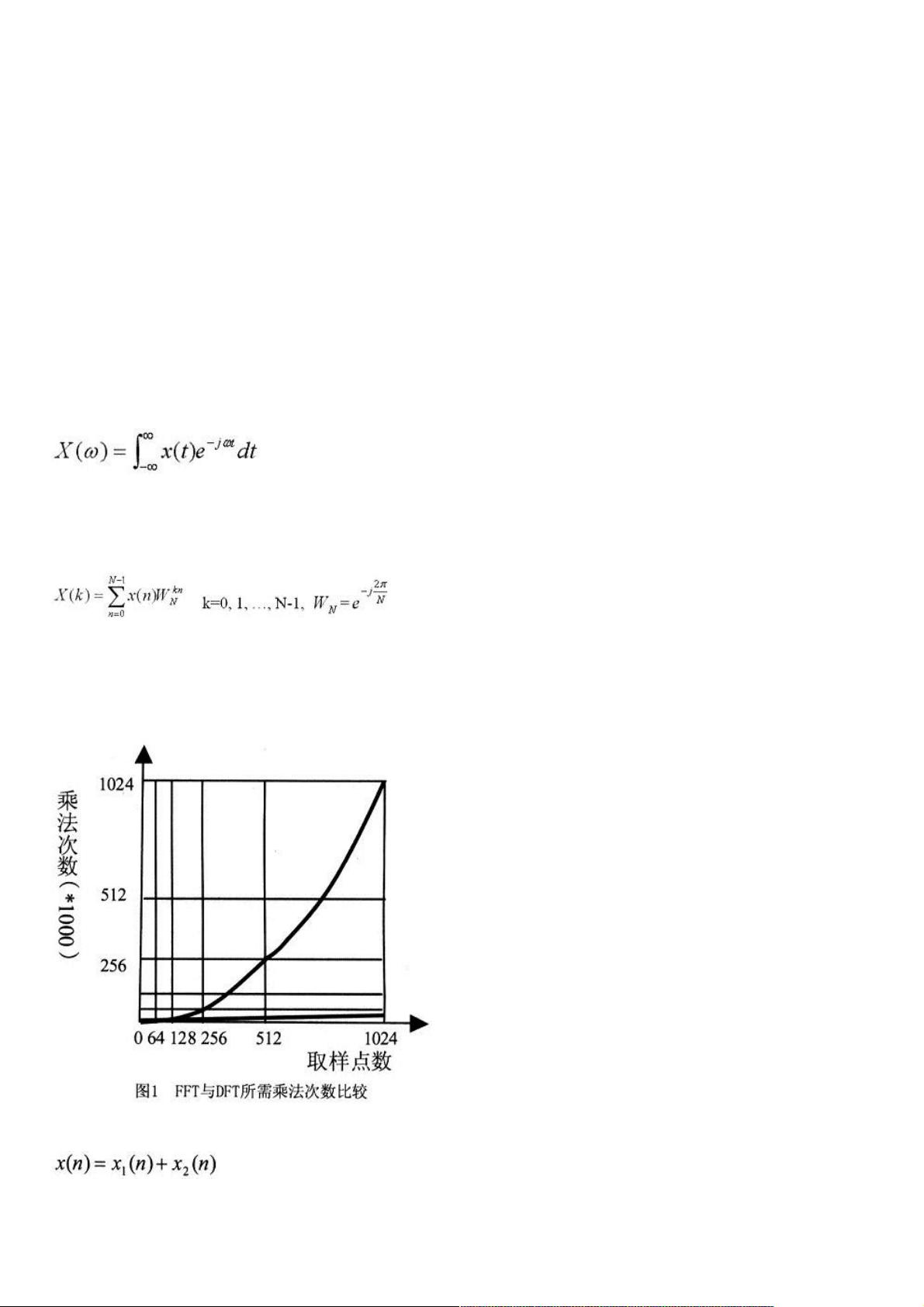
"本文主要探讨了基于TMS32OLF24O7的FFT算法的实现，该算法在TMS320LF2407定点数字信号处理器（DSP）上的应用，展示了其在信号处理和工业控制领域的高效性和可靠性。文章介绍了傅立叶变换在数字信号处理中的重要性，特别是FFT算法如何简化离散傅立叶变换（DFT）的计算，并通过分治策略大幅降低计算量。此外，文章还讨论了DSP为何适合执行FFT运算，以及FFT算法的计算流程和优势。" 快速傅里叶变换（FFT）是一种高效的算法，用于计算离散傅立叶变换（DFT），广泛应用于信号分析和处理。在TMS320LF2407这款定点DSP中，FFT算法能够实现实时、高精度的信号转换，特别适用于那些需要快速频域分析的场景。TMS32OLF24O7是德州仪器（TI）生产的微控制器，具有高性能的 DSP 内核，适用于各种嵌入式应用。 傅立叶变换是将信号从时域转换到频域的关键工具，这有助于揭示信号的频率成分。在时域中难以识别的干扰，如电源噪声，在频域中可以清晰显现。然而，DFT的计算量巨大，不适用于实时处理。FFT通过分解和复用计算，将计算量降低至(N/2)log2N次乘法和Nlog2N次加法，显著提高了效率。 在TMS320LF2407中实现FFT，首先需要将输入序列分为偶数和奇数部分，然后递归地应用FFT，直至处理2点的子问题。这种分治策略使得算法复杂度线性增长，而非平方增长。通过这样的处理，即使在处理大量数据时，也能保持良好的实时性能。 文章中提到，FFT算法在工业控制和信号处理中的应用广泛，包括滤波、频谱分析、通信系统解调等多个领域。TMS32OLF24O7的定点DSP特性确保了运算的精度，同时其高速处理能力满足了实时性需求。因此，基于这种芯片实现的FFT算法不仅有学术价值，而且在实践中也具有广泛的应用前景。 总结来说，基于TMS32OLF24O7的FFT算法实现了高效的数字信号处理，为实时系统提供了强大的分析能力。结合定点DSP的优势，这一实现能够应对各种复杂信号处理任务，为工程师提供了有力的工具，尤其在需要快速频域分析的工业控制和信号处理领域。