算法竞赛树论精华：从基础到高级应用

"这份文件详细介绍了算法竞赛中涉及的树论知识，包括树的基本概念、性质以及相关算法。" 在算法竞赛中，树作为一种重要的数据结构，被广泛应用于解决各种问题。树论是研究树的特性和算法的领域，它涵盖了从基本概念到高级技巧的各种知识。一棵树是由n个顶点和n-1条边组成的无环连通图，其中顶点表示数据，边则表示它们之间的关系。 线段树和树状数组是两种常见的树形数据结构，用于高效地处理区间或段上的更新和查询。线段树通过分治策略将区间问题转化为单点问题，而树状数组则利用差分数组的性质，通过lazy propagation优化更新操作。 树的基础概念包括无根树和有根树。无根树是没有固定根节点的树，而在实际问题中，我们通常会指定一个根节点以简化问题。当为无根树指定一个结点为根时，就形成了有根树。森林是多个树的集合，而生成树则是图的一个子集，包含所有顶点且连接所有顶点但不形成环。 树中结点的属性有深度和高度。深度是指结点到根的路径上的边数，高度是所有结点深度的最大值。无根树的叶子结点是指度数不超过1的结点，而在有根树中，叶子结点是没有子结点的结点。有根树引入了父结点、祖先、子结点、兄弟、后代和子树的概念，这些概念帮助我们更好地理解和操作树的结构。 树的特殊形态如链和菊花树也是树论的重要部分。链是指每结点最多有k条边的树，而菊花树则是一棵树中有一个结点与其他所有结点相连的结构。这些特殊形态的树在某些特定问题中具有特别的应用。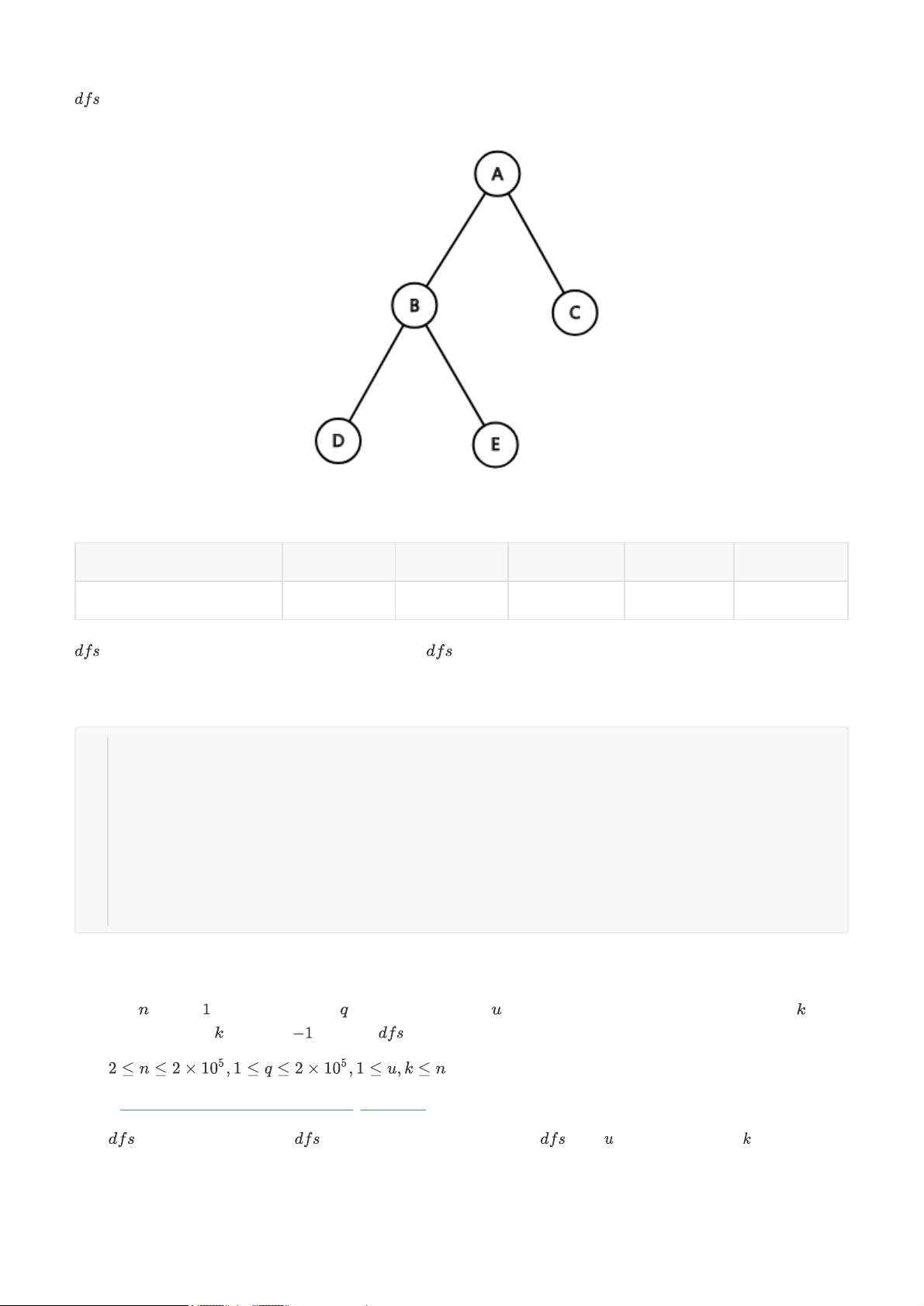 例如，在给定的例题中，你需要通过询问来确定一棵满叉树的根。满叉树是指每个非叶节点都有k个子节点的树。通过询问路径上是否经过特定结点，可以逐步缩小根的可能范围，最终确定根结点。 在算法竞赛中，理解和掌握树论知识至关重要，因为它可以帮助参赛者解决复杂的问题，如求解最短路径、查找最近公共祖先、计算树的直径、进行树的遍历等。熟练运用树的性质和算法，可以显著提高解题效率和正确率。因此，深入学习并实践树论是提升算法能力的关键步骤。