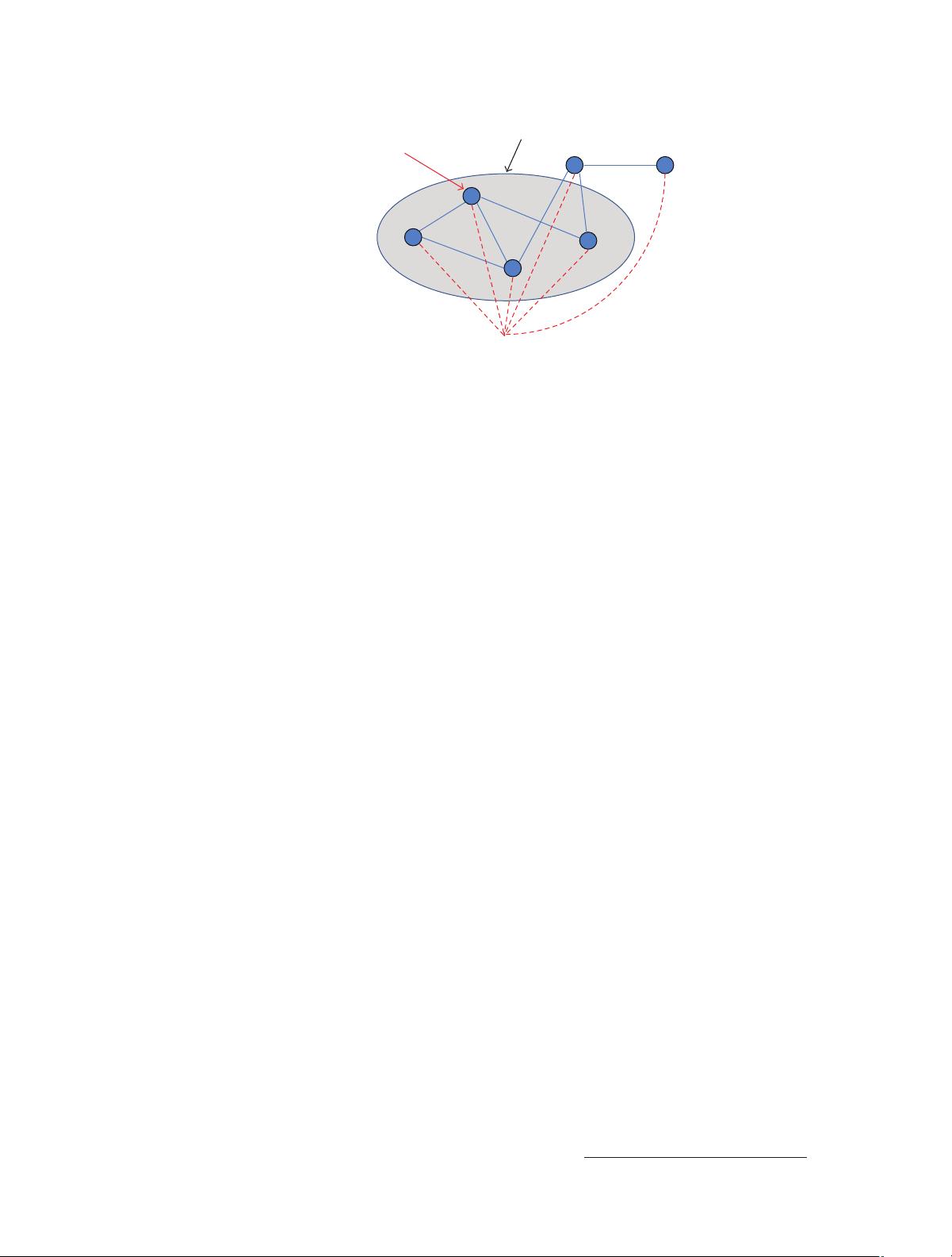
International Journal of Distributed Sensor Networks
Neighbors of node j, Γ
j
Input vectors, X
j
={x
j
l
}
Reproduction alphabet, A={y
i
}
2
1
3
45
j
⌣
F : e graphical representation of distributed vector quantization problem.
() For each input vector , nd the nearest reproduction
vector
𝑖
in reproduction alphabet and assign to
partition
𝑖
:
∈
𝑖
only if ,
𝑖
≤,
𝑗
,∀. ()
() If the total distortion between the input vectors and
their corresponding reproduction vectors of the th
iteration,
𝑚
, is suciently close to that of the (−
1)th iteration,
𝑚−1
,thatis,(
𝑚−1
−
𝑚
)/
𝑚
≤,end
theloop,andusethe
_
𝑚
together with to describe
the vector quantizer. Otherwise, continue.
() For each partition
𝑖
,updatethenewreproduction
vector
𝑖
asthecentroidof
𝑖
:
min
𝑦
𝑖
,
𝑖
|∈
𝑖
.
()
Replace by +1andgotostep-.
In step-, we choose the minimum distortion reproduc-
tion vector for each input. By this step, we get the optimum
partition for the current reproduction alphabet as (). In step-
, we check the ending condition. Alternatively, we can check
whether the partitions between two iterations are changed
because the same partitions mean
𝑚
−
𝑚−1
=0.Instep-
, we get the centroid of each partition to minimize the
distortion in each partition as (). ese steps guarantee that
the total distortion is nonincreasing during the loops and we
can always get a local optimal solution.
3.2. Distributed LBG Algorithm. e traditional LBG requires
that all data are available in a central processor and can be
accessed in their entirety during each iteration. When the
data are distributed over the network and the communication
ability of the sensor network is limited, we need a new
distributed algorithm to solve the distributed vector quanti-
zationproblem.Here,weputforwardourdistributedLBG
algorithm. In brief, each node, in our algorithm, executes
several inner loops of a modied traditional LBG and then
transmits the local results, the reproduction alphabet and the
corresponding partition counts denoted as
_
={
𝑖
,=
1,...,}and ={
𝑖
,=1,...,}, to its neighbors in outer
loops. Each node receives messages from neighbors. en
each node updates the new reproduction vectors by fusing its
local results with the messages from its neighbors. e outer
loops continue until convergence. Aer all nodes stop outer
loops, we collect all the local results to get the nal repro-
duction alphabet. Our idea for distributed LBG algorithm is
borrowed from the distributed -means clustering []. -
means algorithm is similar to LBG algorithm in philosophy.
Clustering wishes to group existing data while quantization
wishes to nd the data structure and uses it on future data.
Here,wemodifythedistributed-means algorithm for vector
quantization, doing some modication for reduction in
communication complexity and improvement in distortion
performance. e detailed explanation is given as follows.
AtthebeginningofourdistributedLBGalgorithm,we
generate the initial reproduction alphabet
_
0
along with a
termination threshold for all nodes in the network. Set
=1and start the loops. For node in iteration of outer
loop, the algorithm is carried out as follows. First of all, we
execute inner loops of the three-step-loops of traditional
LBG with
_
𝑗
𝑚−1
astheinitialalphabet,wheretheinnerloop
parameter is a positive integer. It does not matter whether
the traditional LBG reaches a stable result or not. ese inner
loops use the input data and the reproduction alphabet of
iteration −1of node ,
𝑗
and
_
𝑗
𝑚−1
, to generate the node’s
local alphabet
_
𝑗
𝑚
and the corresponding partition counts
𝑗
𝑚
.
Secondly we enter the outer loop and node transmits its
local results
_
𝑗
𝑚
and
𝑗
𝑚
to its neighbors. Nodes communicate
with neighbors to share their local alphabet and go to next
step when all messages are delivered. irdly each node
updates the reproduction alphabet as a weighted average of
its local alphabet and its neighbors’, and the corresponding
partition counts multiplied by an attenuation coecient work
as the weight factors. e exact formula for fusing result of
𝑗
𝑖
is
𝑗
𝑖
=
𝑗
𝑖
𝑗
𝑖
+exp −/
LBG
∑
ℎ∈Γ
𝑗
ℎ
𝑖
ℎ
𝑖
𝑗
𝑖
+exp −/
LBG
∑
ℎ∈Γ
𝑗
ℎ
𝑖
, ()









