NOMA、mmWave与大规模MIMO融合系统容量深度分析
58 浏览量
更新于2024-08-27
收藏 1.06MB PDF 举报
本文档深入探讨了非正交多址（NOMA）与毫米波（mmWave）以及大规模多输入多输出（massive MIMO）技术在第五代移动通信系统中的融合潜力，针对这一新兴组合进行容量分析。NOMA是一种能提高网络容量和效率的关键技术，通过在同一频带内同时服务多个用户，实现非线性复用。mmWave频段的高带宽特性使得数据传输速率显著提升，而massive MIMO则通过增加天线数量来增强信号的空间分集增益，进一步改善通信质量。
首先，作者提出了一种简化版的mmWave通道模型，基于均匀随机单径模型并考虑了到达角度的影响，以更准确地模拟实际的无线环境。这种模型对于理解信号传播特性和干扰管理至关重要。
接着，论文将容量分析分为两个主要阶段：低信号噪声比（SNR）和高SNR区域。在低SNR环境下，NOMA的性能优势可能被噪声抑制，此时，系统的优化策略主要集中在噪声管理上，如功率分配和信号解码算法的选择，以最大化用户信道容量的利用。
而在高SNR条件下，由于信号强度的相对较强，干扰的影响较小，大规模MIMO的阵列增益成为主导因素。此时，论文可能会探讨如何通过空间多址（Spatial Multiplexing）和空间多工（Spatial Division Multiple Access）来进一步提升系统容量，以及如何平衡多个用户的公平性问题。
此外，论文可能还讨论了mmWave-massive MIMO-NOMA系统中的动态调度、资源分配和用户接入策略，这些都直接影响着系统整体的容量上限。通过对这两种关键技术的结合，研究者试图揭示它们如何协同工作以克服潜在的挑战，如高路径损耗、高多径衰落和用户间信道不均衡。
这篇研究论文提供了一个全面的视角，旨在填补NOMA、mmWave和massive MIMO技术在融合系统中的容量分析空白，并为未来5G和后续通信系统的设计和优化提供了有价值的理论依据。通过深入了解这些技术的交互作用，本文的工作有助于推动无线通信技术的发展，提高网络效率和用户体验。
1608 IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 35, NO. 7, JULY 2017
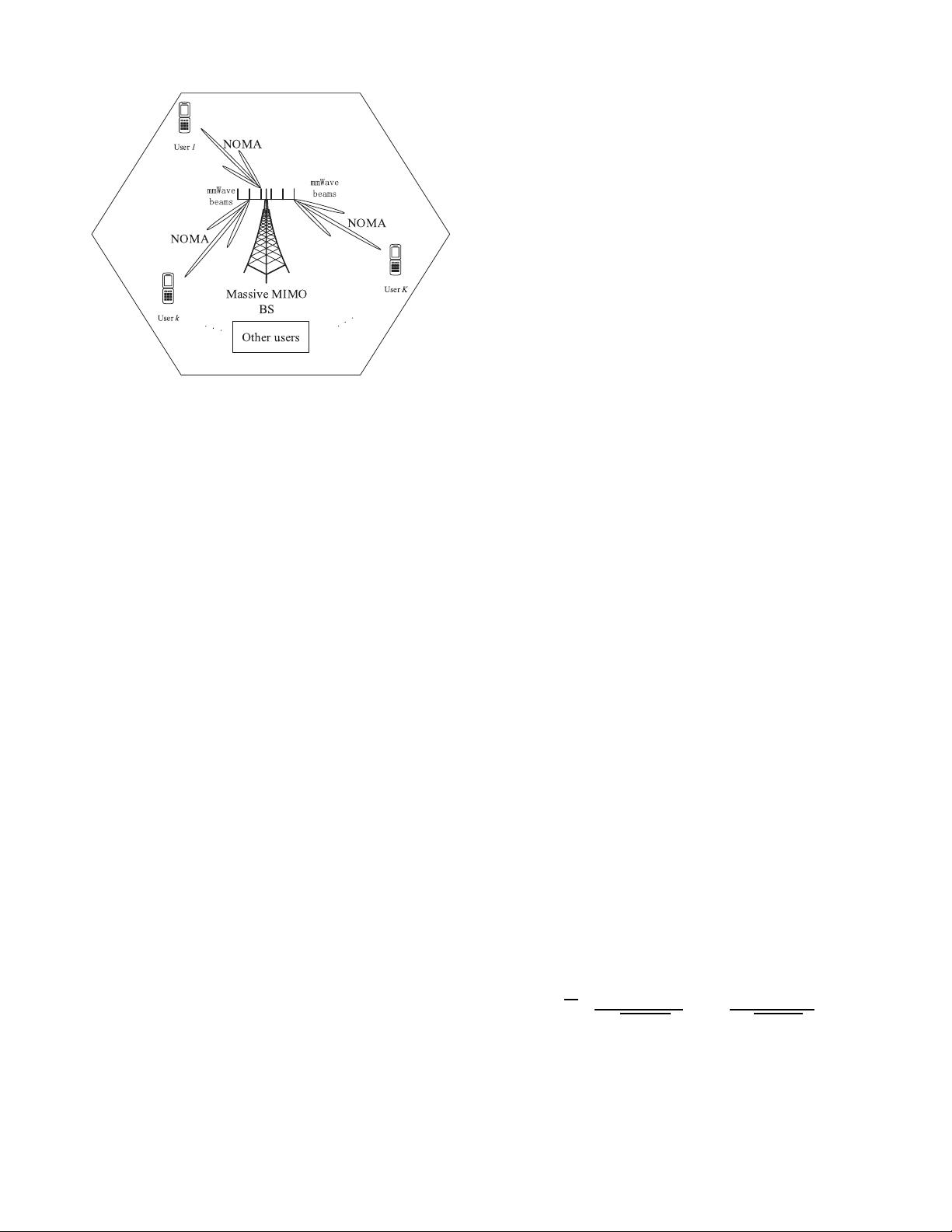
Fig. 1. The conceptual model of the NOMA-mmWave-massive-MIMO
systems.
II. SYSTEM MODEL
In this section, firstly, the NOMA-mmWave-massive-MIMO
systems model in the downlink is elaborated. We further
propose a simplified mmWave channel model by extending
the UR-SP model with AoA and express it in matrix form.
A. The NOMA-mmWave-Massive-MIMO Systems’ Model
The NOMA-mmWave-massive-MIMO systems’ model in
the downlink that focused by this study is shown in Fig. 1.
It consists of a massive MIMO BS that serving less but
multiple user terminals (with number K ). As shown here, the
transmission is carried out in the mmWave frequency with
mmWave beams. In addition, within each beam, the NOMA
encoding scheme is utilized to encode the transmit signal.
With NOMA encoding scheme, the same spectrum resource
block [13] is shared by multiple users within the same user
group (it is assumed that the NOMA users within each
frequency resource block is one user group). Among different
user groups, orthogonal frequency correlations are assumed
to isolate the inter-channel interference. The optimal power
allocation problem of NOMA-MIMO has been investigated by
prior studies [15], [39]. In this paper, we focus on the capacity
analysis of the proposed NOMA-mmWave-massive-MIMO
systems by assuming that power value is different amongst
different users with regards to the NOMA concept [27]. This
is due to the fact that the optimal power allocation study based
on the scenario that the transmission rate requirement of each
user is given beforehand [15], [39]. In addition, this capacity
expression can also be applied for the optimal power allocation
scenario while giving the transmission rate requirement of
each user and the component carrier (CC) bandwidth. The
optimal power allocation study can be done in future based
on the NOMA-mmWave-massive-MIMO system s’ model.
At the receiver side, user can make use of SIC [27], [40]
to remove the interferences from other users with higher
orders. The remaining information from low order users is
treated as interference.
1
With perfect orthogonal characteristics
among channels of different user groups, the inter-channel
interference caused by users in different groups can be ignored.
Thus co-channel interference is mainly from users in the same
group with a lower order.
With mmWave frequency in hand, much wider bandwidth
can be allocated compared with macro wave frequency used
by LTE and prior generations. It was estimated that the
CC bandwidth can be up to 1 GHz or even more with
mmWave [43]. In line with Shannon theory for achievable
transmission rate, with better channel condition, wider CC
bandwidth will yield faster rate. The 5G’s claiming rate can
be easily met with mmWave in this regard, albeit the specific
frequency allocation and usage method of mmWave in 5G
is still on discussion with international telecommunications
union-radio communication (ITU-R).
Assuming the NOMA power allocation for each user
as P
i
, i ∈[1, K ], the received signal is given by
y = H
H
x +n =
K
i=1
P
i
H
H
s +n (1)
where H ∈ C
N×K
is the channel model from N transmit
antennas to K user terminals, x ∈ C
N×1
is the transmit
information at the transmit side, which consists of the transmit
signal s
i
as well as the transmit power P
i
. In addition,
n ∈ C
K ×1
yields the additive white Gaussian noise (AWGN).
Moreover, without loss of generality, it is assumed that
N ≥ K . This is due to the fact that the transmit antenna
number is usually larger than the receive antenna number in
massive MIMO systems. It is also assumed that the transmit
signal s is normalized, which means that each column of s
obeys E[s
i
]=0, and E[s
i
s
H
i
]=1.
With this model in hand, to determinate the capacity
performance of NOMA-mmWave-massive-MIMO systems,
the channel model should be set forth. Given a constant nor-
malized noise value within the channel assumption, capacity
performance is largely determined by the allocated power to
each user and the channel model [2].
B. The Proposed MmWave Channel Model
In line with prior studies from [12], [44], the mmWave
channel model with a three dimensional (3D) transmission
background has to take into consideration the channel gain,
the AoD at the transmitter, and the AoA at the receiver. Taking
an example, the mmWave channel response for the k-th user
can be given as
h
k
=
√
N
⎧
⎨
⎩
β
0
k
d(θ
0
k
)a(φ
0
k
)
1 + d
β
0
k
k
+
M
i=1
β
i
k
d(θ
i
k
)a(φ
i
k
)
1 + d
β
i
k
k
⎫
⎬
⎭
, (2)
where H =[h
1
,...,h
K
]. Besides, integer k ∈[1, K] is the
user index, and integer i ∈[1, M], the NLOS path index.
β
i
k
denotes the channel gain of user k for the i-th NLOS
1
Note that NOMA decoding order can either with regard to the user
orders [41], or with a reversed order with regard to the SNR [42]. Here in
this study, we focus on the first scheme.
剩余12页未读，继续阅读
2022-07-15 上传
2022-07-14 上传
2022-07-14 上传
2021-10-10 上传
2021-09-30 上传
2021-09-30 上传
2022-07-14 上传
2022-07-15 上传
2021-10-18 上传
weixin_38626473
- 粉丝: 3
- 资源: 927
我的内容管理
展开
最新资源
- 黑板风格计算机毕业答辩PPT模板下载
- CodeSandbox实现ListView快速创建指南
- Node.js脚本实现WXR文件到Postgres数据库帖子导入
- 清新简约创意三角毕业论文答辩PPT模板
- DISCORD-JS-CRUD：提升 Discord 机器人开发体验
- Node.js v4.3.2版本Linux ARM64平台运行时环境发布
- SQLight：C++11编写的轻量级MySQL客户端
- 计算机专业毕业论文答辩PPT模板
- Wireshark网络抓包工具的使用与数据包解析
- Wild Match Map: JavaScript中实现通配符映射与事件绑定
- 毕业答辩利器：蝶恋花毕业设计PPT模板
- Node.js深度解析：高性能Web服务器与实时应用构建
- 掌握深度图技术：游戏开发中的绚丽应用案例
- Dart语言的HTTP扩展包功能详解
- MoonMaker: 投资组合加固神器，助力$GME投资者登月
- 计算机毕业设计答辩PPT模板下载
