理解递归：LeetCode 递归基础教程

"LeetCode 递归教程是一个关于计算机科学中的递归概念的教程，主要摘录了非会员部分的内容，未包含会员专享部分。这个教程适用于已经学习过二叉树和栈基础知识的学习者，旨在帮助初学者理解递归的概念、如何解决递归问题以及如何分析递归算法的时间和空间复杂度。通过学习，你将能更自信地独立解决递归问题并进行复杂度分析。在教程最后的讨论论坛中，你可以提出问题或分享见解，会有专业人士进行回应。" 递归是计算机科学中的一个核心概念，它是一种解决问题的方法，通过一个函数调用自身来实现。在每次递归调用时，函数会将大问题分解成规模更小的同类子问题，直到子问题简单到可以直接求解，然后通过这些子问题的解组合得到原问题的解答。这个过程通常伴随着一个或多个终止条件，以防止无限循环。 1. **什么是递归？它如何工作？** 递归是一种自相似的解决问题策略。它的工作原理是，定义一个函数，在函数内部调用自身来处理规模较小的同类问题。递归通常包括两个主要部分：基本情况（Base Case）和递归情况（Recursive Case）。基本情况是最简单的情况，可以直接解决；递归情况是将问题分解并调用自身处理更小规模的问题。 2. **如何用递归解决一个问题？** 解决递归问题的步骤通常是： - 定义基本情况：这是问题最简单、最直接可解的形式。 - 设计递归情况：将问题规模减小，并调用自身处理这些更小的子问题。 - 结合子问题的解：递归调用返回的结果需要组合起来，形成原问题的解答。 - 检查边界条件：确保不会出现无限递归。 3. **如何分析递归算法的时间和空间复杂度？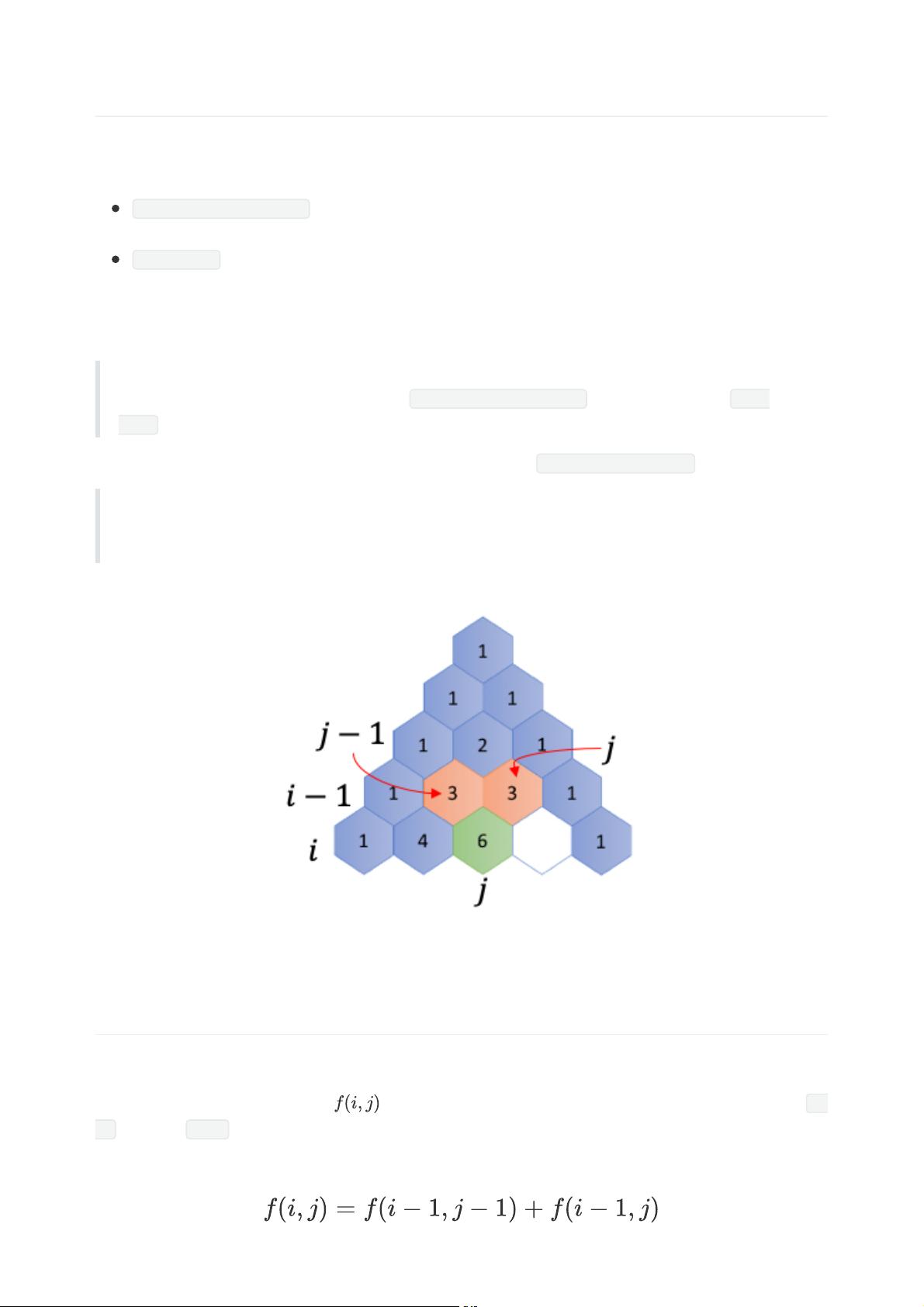** 分析递归算法的复杂度，通常使用“主定理”或“递归树方法”。时间复杂度关注于递归调用的次数，而空间复杂度关注于递归调用栈的深度。在每次递归调用时，如果问题规模减小的量是固定的，那么复杂度可能是线性的或指数的。例如，斐波那契数列的直接递归实现具有指数级的时间复杂度，而使用备忘录或动态规划可以优化到线性。 4. **如何更好地应用递归？** - 避免无谓的计算：使用记忆化（memoization）或动态规划存储已计算过的子问题结果，避免重复计算。 - 确保终止条件明确：避免无限递归。 - 限制递归深度：过深的递归可能导致栈溢出，可以通过尾递归优化或者迭代方法替换。 - 分析和优化复杂度：理解递归算法的运行机制，对时间、空间复杂度进行评估，尽可能降低复杂度。 通过LeetCode的这个递归教程，你将深入理解递归的本质，学会如何运用递归解决实际问题，并提升在面试和实际开发中使用递归的能力。同时，不断实践和分析递归问题，将使你更加熟练掌握这一重要工具。