communication protocols. We only study the duty cycling
of the sensing device. The transceiver does not necessarily
have the same duty cycle with the sensing device. The
consequent advantage is the flexibility for our protocol to
work with different communication protocols. It is
important to note that a sensor node can actually be
attached with multiple sensing devices of different types.
For simplification, however, we assume that a sensor node
is equipped with a single sensing device throughout the
analysis and the protocol design. Nevertheless, they can be
easily extended to support the situation where a sensor
node has multiple sensing devices. Later, we call a sensor
node just a sensor for short if it is not confused with the
sensing device.
In the analysis, we consider a simple algorithm, in which
each sensor wakes up periodically, once in every cycle. In
the rest of the cycle, the sensor stays in power-save mode.
The wakeup selection is random and independent of other
sensors. We refer to this algorithm as RIW. We are inter-
ested in low duty-cycled sensor networks. Thus, we can
safely assume that s
on
s
cycle
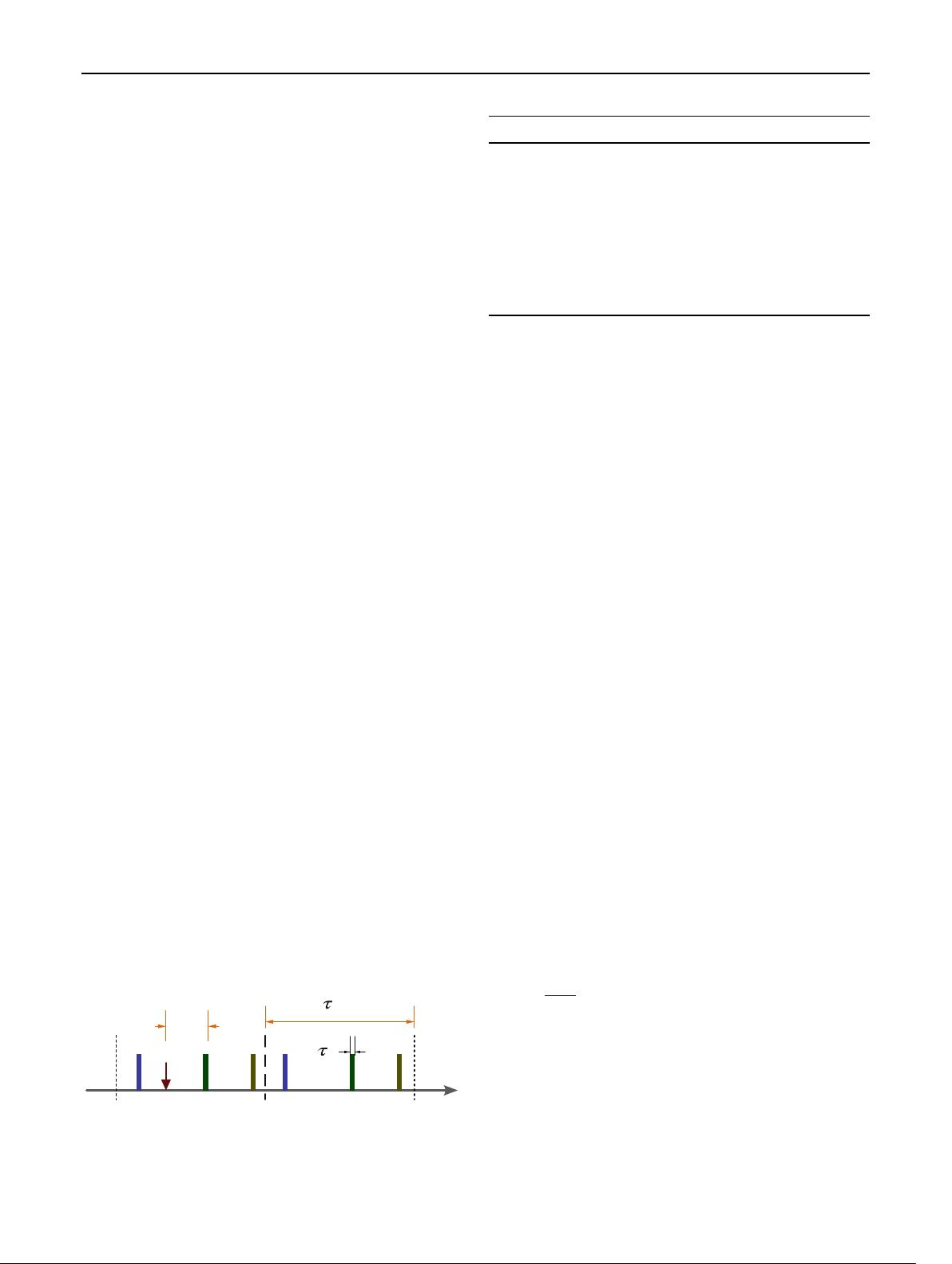
. The example timing of
three sensors with RIW is shown in Fig. 1.
The detection delay of an event, denoted by D,is
defined as the amount of time elapsed from the instant
when the event occurs to the instant when the first sensor
detects it. D is a random variable because the factors that
determine the delay, such as event arrival time, covering
sensors and their wakeups, are all unpredictable. The
detectability of an event with duration t is the probability
that it can be detected by at least one sensor. The detect-
ability of an event is 100% if its duration exceeds the
sensor cycle. Although events are usually persistent, we
still study the detectability of an event whose duration is
shorter than the sensor cycle since it reflects the capability
of the network to capture events. We study the detection of
any event that occurs anywhere within the field and arrives
at any time.
In the rest of this paper, we adopt the notations shown in
Table 1 and make the following assumptions.
2.1.1 Binary detection model
Each sensor has a sensing range. An event is reliably
detected by an active sensor if its distance to the sensor is
less than the sensing range. More sophisticated models
suggest that the detection probability is related to the dis-
tance between the sensor and the event. For simplification,
we assume that the sensing range is selected such that an
event can be detected with high probability if its distance to
the sensor is less than the sensing range.
2.1.2 Time synchronization
We assume the time synchronization mechanism is avail-
able for loose time synchronization. Protocols for clock
synchronization in sensor networks can be found in [26]. It
has been reported that accuracy on the order of millisec-
onds can be achieved.
2.1.3 Stationary events
After an event has occurred, it remains at the location
where it happens. In some cases, events are caused by
moving objects. As long as the moving speed of objects is
slow, our approach can still apply. If objects move fast,
sensors have no choice but keep active all the time.
2.2 Theoretical analysis of event detection
We analyze detection delay and detectability given a fixed
sensor cycle. Since s
on
s
cycle
, we firstly assume that s
on
is negligible for analysis simplicity. The complete analysis
with consideration of s
on
follows.
Lemma 1 A point is covered by k sensors, and their
wakeups are fixed values w
i
, and w
i
w
iþ1
, 1 i k 1.
The delay expectation of any event at this point is
Eð DÞ¼
1
s
cycle
X
k
i¼1
w
2
i
X
k
i¼1
w
i
w
ðiþ1Þmodk
ðw
1
w
k
s
cycle
=2Þs
cycle
!
:
ð3Þ
Note that in Lemma 1, we fix both the set of covering
sensors and their wakeups. Next, we relax the assumption
of fixed wakeups and give Lemma 2.
A
BC
cycle
on
Time
Event
delay
Fig. 1 Example timing of three sensors with RIW
Table 1 Main notations adopted in this paper
Notation Description
R
s
The sensing range
R
t
The communication range
n Initial amount of energy on every sensor node
Pr(E) The probability that event E occurs
E(X) The expectation of random variable X
l The expectation of detection delay
r The standard deviation of detection delay
v(t) The detectability of an event with duration t
Wireless Netw (2012) 18:241–255 243
123









