短时傅里叶变换：时频分析的关键工具

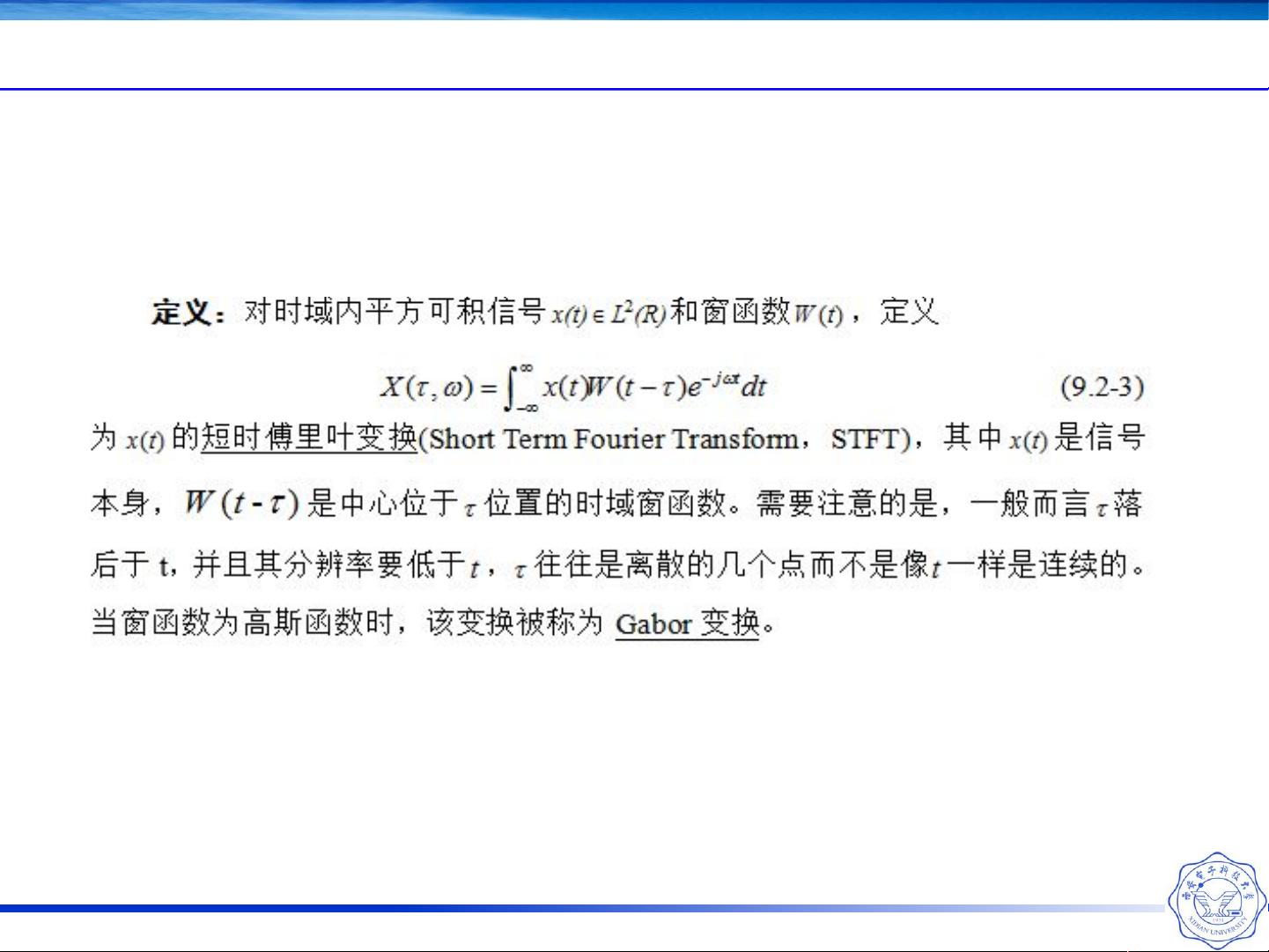
"该资源是关于短时傅里叶变换(Short-Time Fourier Transform, STFT)的介绍，强调了STFT在处理时变信号中的重要性，并提到了STFT的定义、窗函数的作用以及其在不同领域如音乐、地震波分析和图像分析中的应用。" 在数字信号处理领域，短时傅里叶变换是一种非常关键的分析工具，它弥补了传统傅里叶变换在处理非平稳信号时的不足。传统傅里叶变换能够提供信号的全局频率分布，但无法揭示信号在时间上的变化。相反，短时傅里叶变换通过将信号分割成一系列短的、重叠的子序列（也称为窗口），然后对每个子序列分别进行傅里叶变换，从而可以同时获取信号在时间和频率上的信息。 STFT的定义是：对于一个信号x(t)，选择一个窗函数g(t)，将信号与窗函数相乘得到局部化的信号x(t)g(t)，然后对这个乘积进行傅里叶变换，得到的就是信号在该时间窗口内的频率特性。窗函数的选择至关重要，因为它影响到分析的时频分辨率。通常，更窄的窗函数会提供更好的频率分辨率，但牺牲了时间分辨率，反之亦然。 短时傅里叶变换的一个显著特点是结果的对称性，这源于其计算过程中的傅里叶变换性质。STFT的结果通常显示为时频谱，可以清晰地显示出信号中各个频率成分在时间上的出现和消失，这对于识别和分析非平稳信号的特征极其有用。 在实际应用中，STFT广泛应用于多个领域。例如，在音乐和语音信号分析中，STFT可以帮助识别特定音符出现的时间点；在地震学中，它可以定位不同频率的反射波发生的地点；在图像分析中，它可以用于检测信号突变的位置，比如边缘检测。 多分辨率分析是STFT的一个相关概念，它允许我们根据需要调整分析的精细程度，从而更好地捕捉信号的细节。通过改变窗函数的大小，可以在不同的时间尺度上分析信号，这对于理解和解释复杂信号的行为非常有帮助。 短时傅里叶变换是理解和解析时变信号的强大工具，它提供了信号在时频空间的分布，使得工程师和研究人员能够深入洞察信号的本质特征，从而进行更精确的分析和处理。学习和掌握STFT及其应用对于任何从事信号处理相关工作的专业人士都至关重要。