生物启发的深度学习：脉冲神经网络的挑战与进展

需积分: 0 56 浏览量更新于2024-06-22 收藏 1.04MB PDF 举报

"本次综述文章探讨了脉冲神经网络（SNN）和生物启发式监督深度学习在人工智能领域的应用，旨在提供一个全面的视角来理解这两种方法的最新进展和挑战。作者首先介绍了生物神经元的基本计算原理和突触可塑性，然后深入到SNN模型的细节，讨论了其在训练过程中的独特问题。此外，文章还讨论了替代传统反向传播的生物启发式训练策略，以及如何通过生物启发的深度学习（BIDL）提升模型的计算性能和生物可信度。" 在人工智能领域，生物神经科学的研究为计算机科学家提供了丰富的灵感。脉冲神经网络（SNN）是模拟大脑神经元活动的一种模型，它以脉冲（或尖峰）的形式进行信息传递，更加接近生物神经系统的运作方式。SNN的优势在于其高效的能量消耗和时间编码能力，但与传统的基于连续数值的神经网络不同，SNN的训练通常需要解决反向传播不适用的问题。这导致了对新的训练方法的需求，例如那些受到生物过程启发的策略。文章详细介绍了SNN模型的不同方面，包括它们如何模拟神经元的电生理特性，如 leaky integrate-and-fire (LIF) 模型，以及它们如何模拟突触权重的动态变化。在SNN的训练过程中，由于尖峰的时间序列和非连续性，传统的反向传播算法无法直接应用。因此，研究人员提出了各种生物启发式的训练方法，这些方法试图模拟生物学习规则，如 STDP（突触时间依赖性可塑性），在SNN中实现权重更新。生物启发的深度学习（BIDL）方法是针对这一挑战的解决方案之一。这些方法不仅关注模型的性能，还注重其生物现实主义，即模型的行为和学习机制应尽可能地接近生物神经系统。BIDL试图在保持高性能的同时，提高模型的生物可信度，从而推动AI技术向更真实的神经计算模式靠拢。总结来说，这篇综述文章提供了关于SNN和BIDL的深入洞察，涵盖了这些领域的最新研究进展和未来可能的发展方向。对于那些对生物启发式AI方法感兴趣的读者，这篇文章提供了一个宝贵的资源，帮助他们理解和利用这些技术来改进现有的神经网络模型和算法。

6 Lagani, et al.

Note that, more in general, local learning rules with higher order interactions can be considered. A general form for

such a local synaptic update equation, for a generic synaptic connection 𝑖, can be expressed as [61]:

Δ𝑤

𝑖

= 𝑎

+ 𝑎

𝑥

𝑖

+ 𝑎

𝑦 + 𝑎

𝑥

𝑖

𝑦 + 𝑎

𝑥

𝑖

+ 𝑎

𝑦

+ ... (4)

where the coecients 𝑎

𝑖

may depend on the weights.

When multiple neurons are involved in a complex network, it is desirable that dierent neurons learn to recognize

dierent patterns. In other words, neural activity should pursue a decorrelated form of coding [

154

], in order to

maximize the amount of information that neurons can transmit. This can be achieved by leveraging the biological

mechanisms of lateral and inhibitory interaction. For example, Eq. 3 can be coupled with competitive learning mechanisms

such as Winner-Takes-All (WTA) [

178

]: in this case, the neuron with strongest similarity to a given input is chosen

as the winner, and it is the only one allowed to perform a weight update, by virtue of lateral inhibition [

]. In this way,

if a similar input will be presented again in the future, the same neuron will be more likely to win again, and dierent

neurons will specialize on dierent clusters. Other forms of lateral interaction can also enable a group of neurons to

extract further principal components form the input (subspace learning) [15, 93, 180].

As a further extension of PCA-based learning methods, Independent Component Analysis (ICA) aims at removing

higher-order correlations from data [

162

]. Sparse Coding (SC) [

154

] is another principle, strictly

related to ICA [

153

], from which biologically plausible HaH feature learning networks can be derived, as in the Locally

Competitive Algorithm (LCA) [175].

Hebbian approaches based on competitive [

102

108

137

141

207

] or subspace learning [

104

109

] have

recently been subject of signicant interest towards applications in DL contexts.

4 SPIKING NEURAL NETWORKS

This Section discusses models of neural computation based on Spiking Neural Networks (SNNs) [

], which more

faithfully resemble real neurons compared to traditional ANN models. We start by introducing the various neuron

models for SNN simulation. We highlight the applications related to biological and neuromorphic computing, which are

of strong practical interest thanks to the energy eciency of the underlying computing paradigm, and we discuss the

challenges related to SNN traning. We describe the biological plasticity models for spiking neurons, and the approaches

to translate backprop-based training to the spiking setting. Finally, an overview of some existing experimental results is

given.

In the following, subsection 4.1 illustrates the main models of spiking neurons and spike-based strategies for

information encoding; subsection 4.2 highlights promising applications of spiking models in the eld of neuromorphic

and biological computing, and the challenges of learning with spiking models; therefore, subsection 4.3 discusses the

plasticity models for spiking neurons, based on Spike Time Dependent Plasticity (STDP); nally, subsection 4.4 presents

some experimental results from literature regarding the applications of SNNs and STDP in DL contexts.

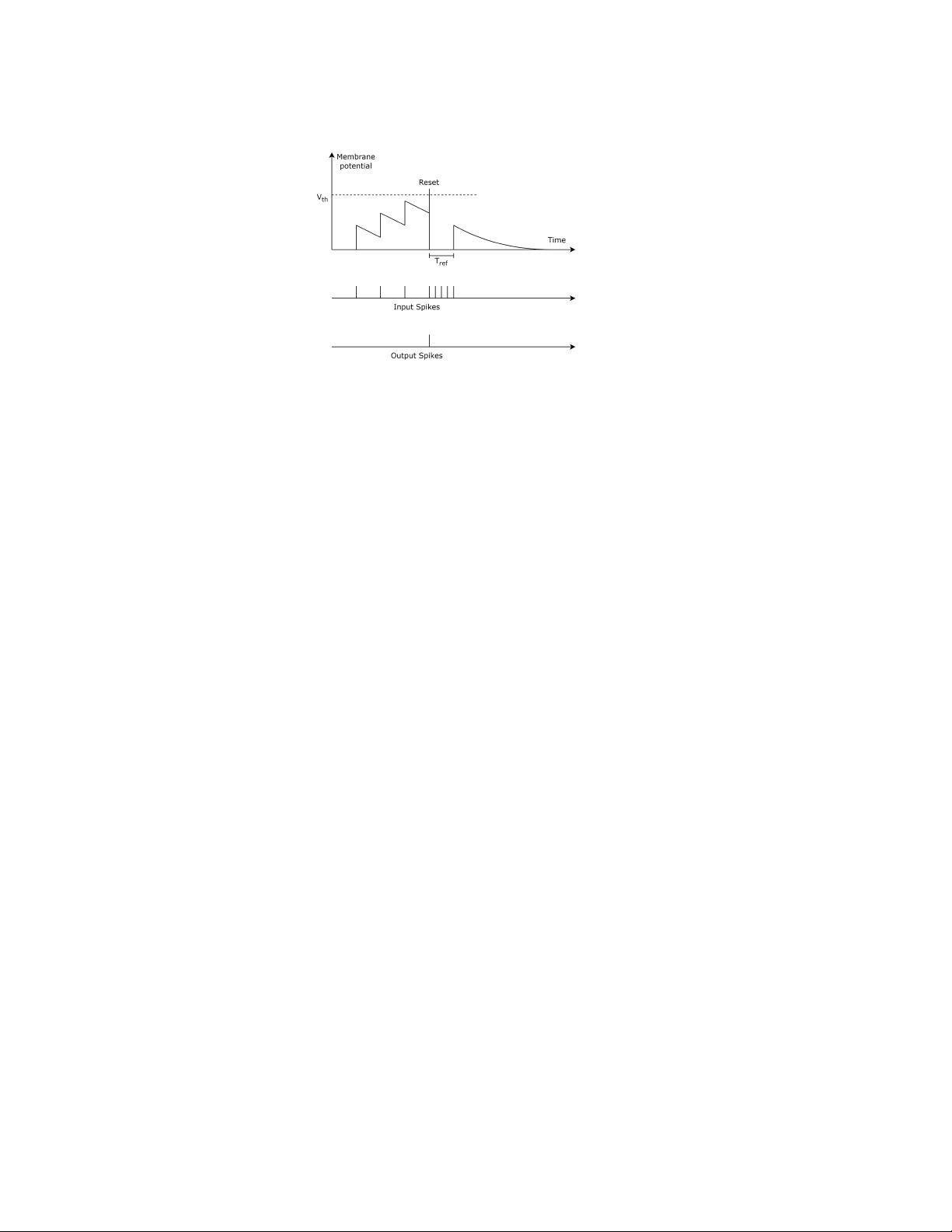
4.1 Spiking Neuron Models and Spike Codes

Spiking Neural Networks (SNNs) are a realistic model of biological networks [

126

]. While in traditional Articial

Neural Networks (ANNs), neurons communicate via real-valued signals, in SNNs they emit short pulses called spikes.

All the spikes are equal to each other and values are encoded in the timing or in the frequency with which spikes are

emitted.

Various spiking neuron models have been proposed in literature [61], which we highlight in the following:

Manuscript submitted to ACM

Bio-Inspired Deep Learning 7

Fig. 3. Behavior of a LIF unit.

•

Hodgkin-Huxley (HH) model [

] is a classical and low-level description of the processes that regulate the neuron

behavior, in terms of nonlinear dierential equations. This model is very detailed, but also computationally

expensive to simulate.

•

Izhikevich model [

] is less detailed but also computationally more ecient to simulate. It is based on a simplied

description of the neuron behavior, compared to HH equations, but still retaining the main elements that allow

to simulate a variety of observed neural behaviors, such as bursts of activity or sustained oscillations.

•

The Spike Response Model (SRM) [

] is a higher-level description that describes the state of a neuron in terms

of the electric potential accumulated on its neuronal membrane. Two kernels are dened which represent the

eect of, respectively, incoming and outgoing spikes on the membrane potential. Appropriate choice of such

kernels allows to simulate a variety of neuron behaviors.

•

The Leaky Integrate and Fire (LIF) model [

] is probably the most abstract description of spiking neurons, as

well as the most computationally friendly for simulations.

LIF neurons represent an ideal trade-o between biological accuracy and eciency of simulation, when it comes to

modeling complex spiking neural systems. For this reason, the LIF model is widely used in practice for the simulation

of large-scale SNN architectures. In the following, we describe the LIF neuron model in more detail. LIF neurons behave

like integrators, summing up all the received spikes (weighted by the synaptic coecients) until a threshold is exceeded.

At this point, an output spike is emitted (Fig. 3). In practice, this integration logic is implemented in terms of an electric

potential that is accumulated on the neural membrane every time an input spike is received; when the threshold is

reached and the output spike is released, the neural membrane discharges the accumulated potential and the process

restarts. Immediately after the discharge, the neuron enters its refractory period, a time interval where it cannot spike

regardless of its input. These units are leaky in the sense that, when no spikes are received in input, the membrane

potential decays exponentially.

Notice that the neural computation discussed above is deterministic, but extensions of neuron models to the stochastic

setting also exist [

], which are better suited to model noisy scenarios. Specically, there are two approaches to

inject randomness in spiking models: noisy thresholds (or escape noise) and noisy integration (or diusive noise). In noisy

threshold models, the neuron doesn’t re deterministically when the threshold is overcome, but it res stochastically,

with a probability density that depends on the current value of the membrane potential itself (the higher the value, the

Manuscript submitted to ACM

剩余30页未读，继续阅读

学术菜鸟小晨

粉丝: 1w+
资源: 5534

生物启发的深度学习：脉冲神经网络的挑战与进展

Spiking neural networks

Time-Space, Spiking Neural Networks and Brain-Inspired Artificial Intelligence

Synaptic Plasticity Models and Bio-Inspired Unsupervised Deep Le

Training-spiking-neural-networks-for-reinforcement-learning:源代码：https

Spiking neural networks.rar_Neural networks_SNN_Spiking-Neural_s

Hebbian Learning in Spiking Neural Networks

藏经阁-Spiking Neural Networks, the N.pdf

Spiking Neural Networks: The Machine Learning Approach

Patio-Temporal Backpropagation for Training High-Performance Spiking Neural Networks.pdf

Spiking Neural Networks for Cortical Neuronal Spike Train Decoding

最新资源