自动控制原理复习：拉普拉斯变换详解

"该资源是北京航空航天大学的精品课程，专注于自动控制原理的复习指导，主要涉及拉普拉斯变换及其在解决控制系统问题中的应用。" 在自动控制领域，拉普拉斯变换是一种重要的数学工具，它在分析线性时不变系统的动态性能时起着核心作用。在【第一讲拉普拉斯变换及其应用】中，课程强调了以下几个关键知识点： 1. 基本要求： - 学习者需要熟悉拉普拉斯变换的基本法则，这是进行系统分析的基础。 - 掌握典型函数如指数函数、阶跃函数等的拉氏变换形式，这些是控制系统中常见的输入和输出信号。 - 理解如何使用拉氏变换来求解微分方程的初值问题，这对于理解和设计控制器至关重要。 - 熟练掌握有理分式函数的拉氏反变换方法，这是解析系统传递函数的关键。 2. 重点讲解： - 拉氏变换的线性性质是其应用广泛的原因，它源于定积分的线性性质。这意味着系统输入和输出的拉氏变换可以通过简单相加得到，这在工程计算中非常实用。 - 然而，拉氏变换的收敛域和主值积分的计算通常不作为重点，因为实践中往往使用查找表来快速完成变换。重点在于正确地应用变换法则。 - 拉氏变换的一一对应关系要求原函数在时间零点为零，这与单位阶跃函数的定义紧密相关。理解这个条件对于正确处理延迟和初始条件问题至关重要。 3. 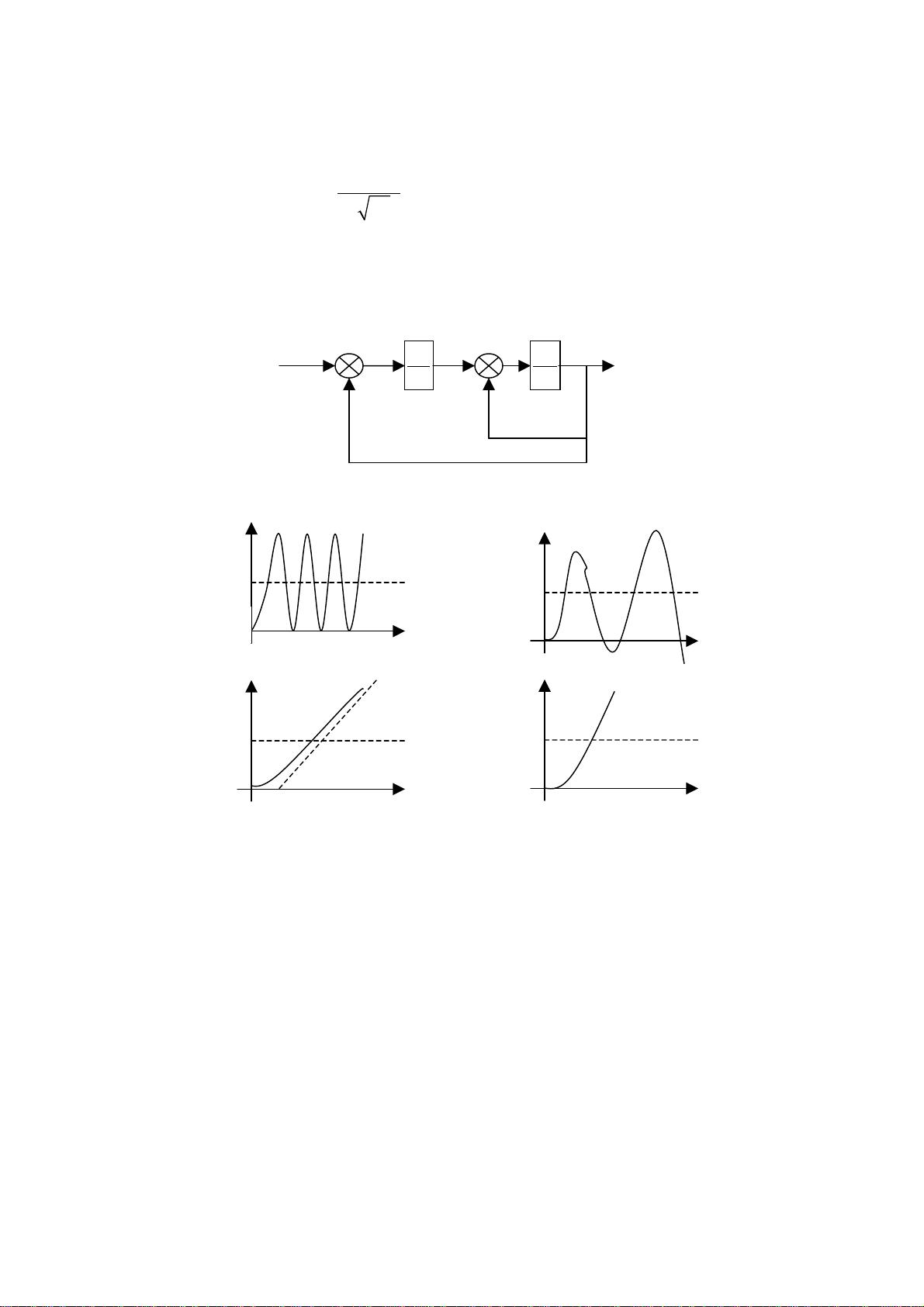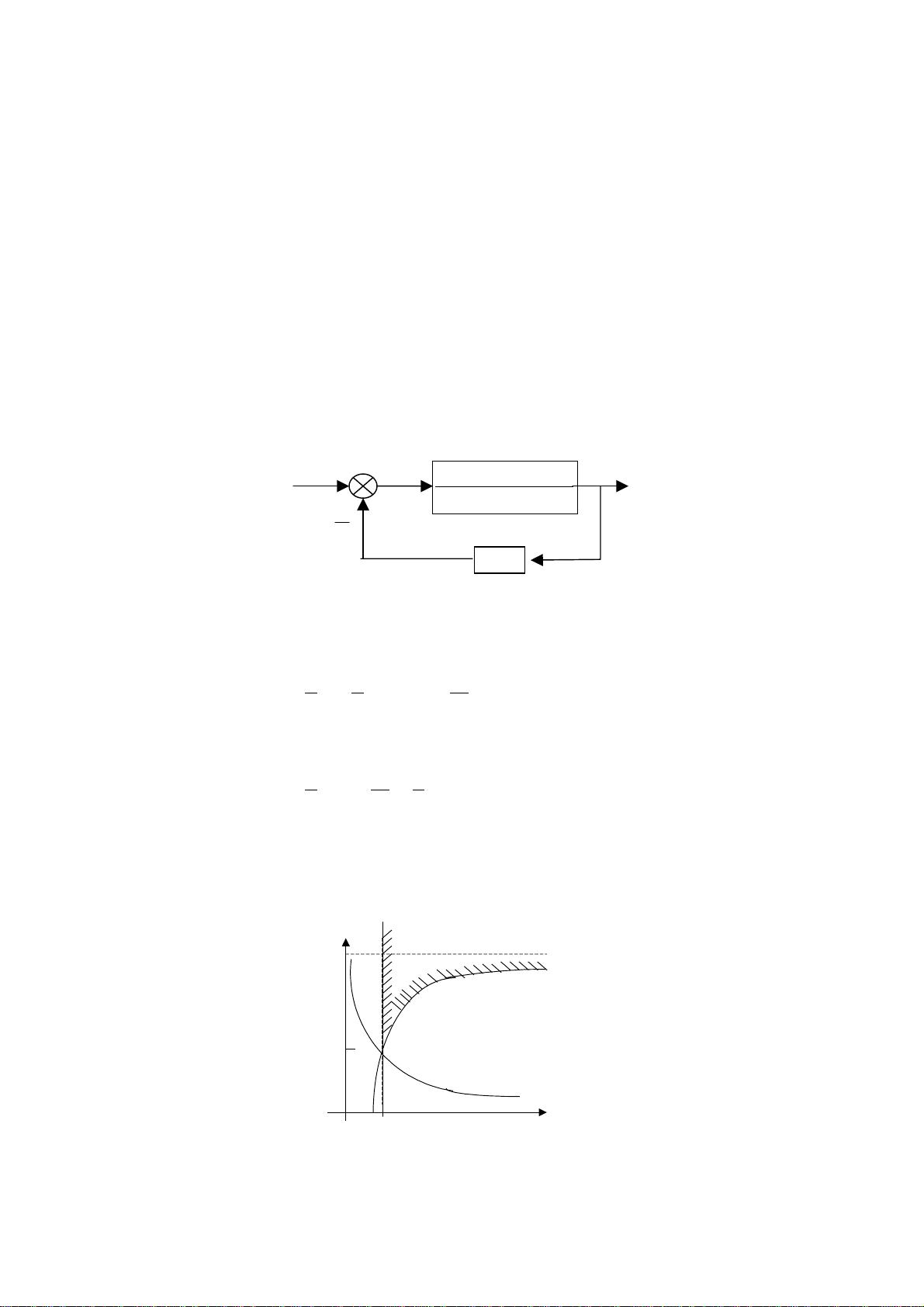延迟与拉氏变换： - 描述信号延迟时，必须确保正确理解函数形式。例如，延迟函数应该表示为与原函数的乘积，而不是简单的平移。课程中通过示例和图形解释了这一点。 - 示例1-2展示了如何根据波形图应用拉氏变换和延迟定理来求解复杂信号的拉氏变换，这是解决实际问题的实际操作训练。 这个课程不仅涵盖了理论知识，还强调了实践应用，通过例题和图形解释，帮助学生巩固概念并提升解决问题的能力。对于希望深入理解自动控制原理和掌握拉普拉斯变换技术的学生来说，这是一份宝贵的资源。