上下文无关文法详解:派生树与文法规则
版权申诉
7 浏览量
更新于2024-07-03
收藏 870KB PPT 举报
"形式语言与自动机理论的第六章主要探讨了上下文无关语言的相关概念。这一章包括了上下文无关文法的定义、化简方法、乔姆斯基范式和格雷巴赫范式,以及自嵌套文法的介绍。其中,上下文无关文法是描述计算机科学中编程语言语法的重要工具。"
上下文无关文法(Context-Free Grammar, CFG)是形式语言理论中的关键组成部分,用于描述一类语言,即上下文无关语言。文法G由四部分组成:一组非终结符V,一组终结符T,一组产生式P,以及一个起始符号S。当文法中的所有产生式满足非空替换时(即除了A→ε这样的产生式外,其他产生式右边的符号串长度至少等于左边的非终结符个数),则称其为上下文无关文法。这种文法的特点在于,可以在不考虑非终结符出现的上下文情况下,将非终结符替换为其相应的产生式。
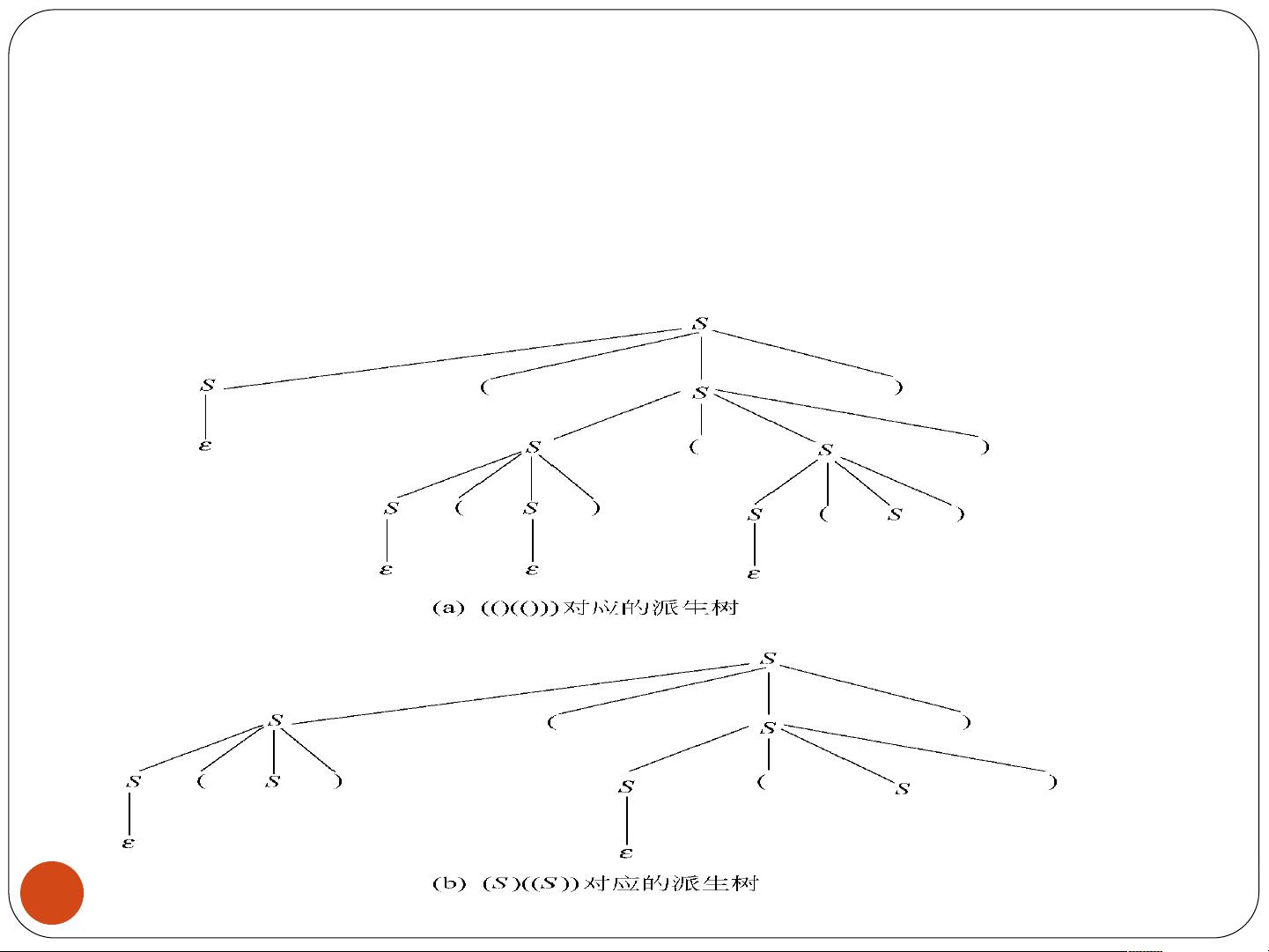
1.1上下文无关文法的派生树是理解文法工作方式的一个重要工具。通过派生树,我们可以直观地看到如何从起始符号生成一个句子。例如,给定一个用于表示算术表达式的文法Gexp1,它包含一系列产生式,用于描述加法、乘法、指数等操作。派生树展示了如何从起始符号E出发,通过应用这些产生式构建出具体的算术表达式,如x+x/y↑2。派生树的不同分支表示了同一句子可能的多种构建方式。
派生树在展示句子结构时,可以忽略具体的替换顺序,只关注最终结果,从而形成更清晰的结构表示。文法Gexp1的派生树揭示了x+x/y↑2这个句子的结构,展示了如何从起始符号S派生出整个表达式。在实际的解析过程中,派生树对于编译器设计和分析程序语法至关重要。
除了上下文无关文法的基本概念,该章还涉及了文法的化简,例如乔姆斯基范式(Chomsky Normal Form)和格雷巴赫范式(Greibach Normal Form)。这些范式简化了文法的结构,使得分析和处理更为方便。乔姆斯基范式要求产生式要么是A→BC,要么是A→a,其中A、B、C是非终结符,a是终结符。而格雷巴赫范式则是每个产生式以一个非终结符开头,后面跟着一个单一的终结符。
此外,自嵌套文法(Nested Grammar)是一种特殊的上下文无关文法,它允许产生式在自己的定义中递归地使用自身。自嵌套文法可以描述一些复杂结构,但可能导致解析的困难。
总结来说,本章深入介绍了上下文无关文法及其相关概念,包括派生树、化简技术以及特殊类型的文法,这些都是理解和处理形式语言的基础,对于计算机科学尤其是编译原理和解析技术领域至关重要。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-10-01 上传
2022-06-17 上传
2022-06-17 上传
智慧安全方案
- 粉丝: 3837
- 资源: 59万+