岭回归分析详解：从定义到参数选择

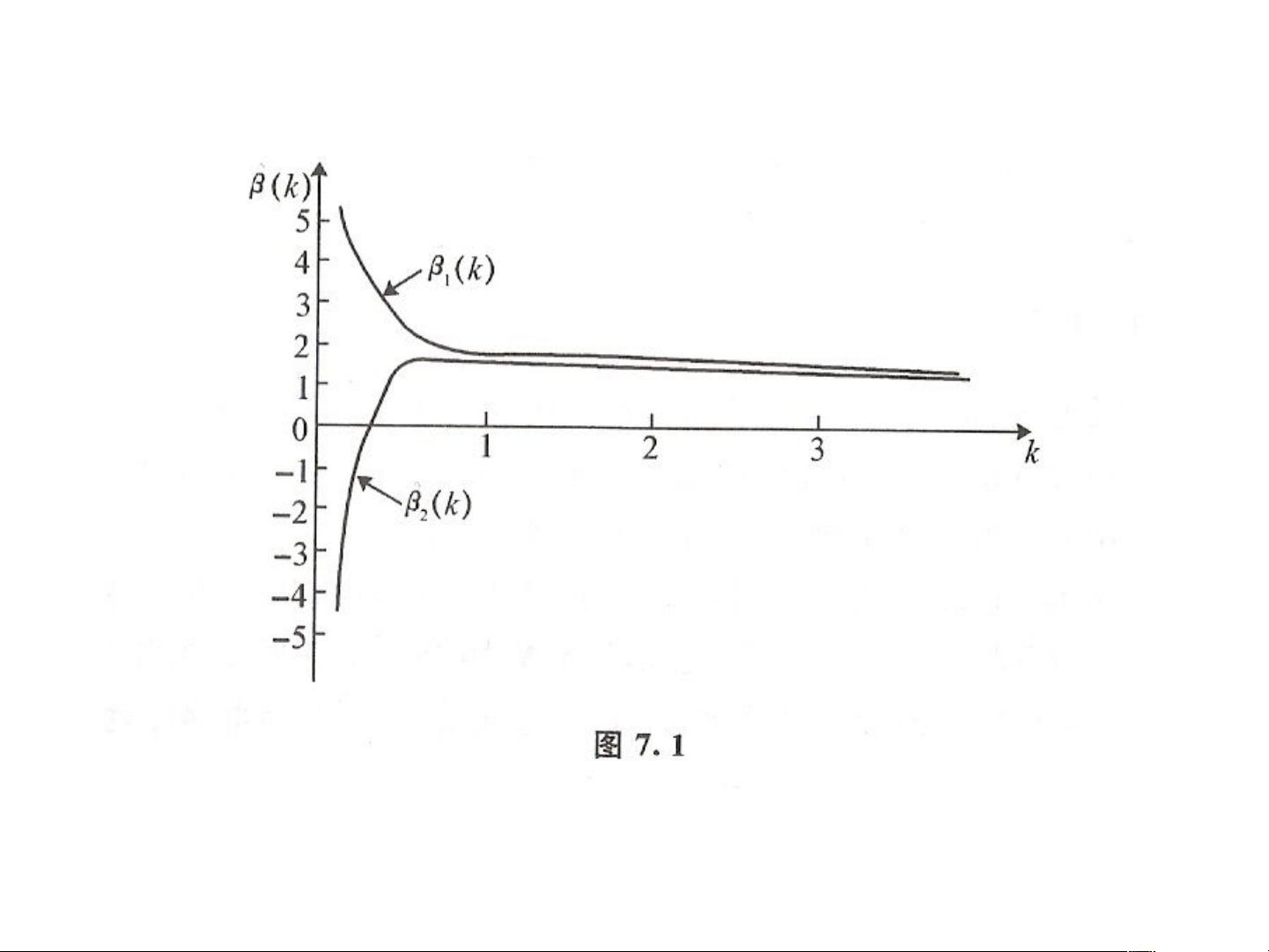
"岭回归分析是一种处理共线性问题的统计方法，主要用于数据点少于变量个数或变量间存在高度相关性的线性回归模型。它通过在最小二乘估计的基础上引入岭参数k，使矩阵X'X+kI更加非奇异，从而提高估计的稳定性。岭回归在牺牲无偏性的同时，提供了更稳健的回归系数估计，增强了对病态数据的容忍度。" 岭回归分析主要包含以下几个方面： 1. 岭回归估计的定义：当自变量间存在共线性导致最小二乘估计不稳时，岭回归通过在X'X矩阵上添加一个正比例的单位矩阵kI来改善。标准化后的岭回归估计公式为 y = Xβ^k -1，其中β^k 是岭回归估计的系数，k是岭参数。 2. 岭回归估计的性质：讨论了当因变量y未经标准化时，岭回归估计的一些特性。这些性质可能涉及到估计的偏置、方差以及与最小二乘估计的比较。 3. 岭迹分析：通过对不同k值下回归系数的变化轨迹进行分析，可以帮助理解岭参数对估计稳定性的影响，并寻找合适的k值。 4. 岭参数k的选择：有多种方法选择最佳的k值，如岭迹法，关注于回归系数的稳定性、符号的合理性以及绝对值的经济意义；方差扩大因子法，通过比较模型的方差膨胀情况来评估；或者根据残差平方和的变化来判断，尽管岭回归会增加残差平方和，但要确保这个增加在可接受范围内。 5. 应用领域：岭回归广泛应用于机器学习和统计学，尤其是在SPSS等数据分析软件中，帮助解决线性模型中的共线性问题，提高模型的预测能力和解释性。 岭回归分析的实施通常包括以下步骤： - 数据预处理：对数据进行标准化，确保所有变量在同一尺度上。 - 计算X'X+kI：根据数据计算添加了kI后的矩阵，调整模型的稳定性。 - 选择岭参数k：通过岭迹分析、方差扩大因子法或其他方法确定最佳的k值。 - 求解岭回归系数：利用优化算法求解带有k的最小二乘问题。 - 模型评估：评估模型的预测性能和系数的稳定性，检查残差性质，如正态性和独立性。 在实际应用中，岭回归不仅可以处理高相关性变量的问题，还可以用于特征选择，通过观察不同k值下的系数变化，识别出对模型贡献最大的变量。岭回归是一种强大的工具，能有效地处理线性模型中的共线性问题，提高模型的稳定性和可靠性。