Effective medium theory of checkboard structures
in the long-wavelength limit
Zhanlei Hao (郝占磊), Yawen Zhuang (庄雅雯), Ying Chen (陈 颖)*,
Yineng Liu (刘益能)**, and Huanyang Chen (陈焕阳)***
Institute of Electromagnetics and Acoustics and Key Laboratory of Electromagnetic Wave Science
and Detection Technology, Xiamen University, Xiamen 361005, China
*Corresponding author: lyn610@xmu.edu.cn; **corresponding author: irusying1218@xmu.edu.cn;
***corresponding author: kenyon@xmu.edu.cn
Received March 16, 2020; accepted April 30, 2020; posted online May 26, 2020
Effective medium theory is a powerful tool to solve various problems for achieving multifarious functionalities
and applications. In this article, we present a concise empirical formula about effective permittivity of check-
board structures for different directions. To verify our empirical formula, we perform simulations of checkboard
periodic structures in squares, rectangles, and sectors in two dimensions. Our results show that the formula is
valid in a large range of parameters. This work provides a new way to understand and design composite materi-
als, which might lead to further optical applications in transformation optics.
Keywords: effective medium theory; checkboard structures; effective permittivity.
doi: 10.3788/COL202018.072401.
Effective medium theory (EMT)
[1]
can achieve similar
functions of overall systems by defining material averages
with effective parameters. There are two famous theories
of effective medium approaches, i.e., the Maxwell– Garnett
theory (MGT)
[2]
and the Bruggeman EMT (BEMT)
[3]
,
which are both based on material characteristics of each
component in the mixture. Depending on the relative con-
centration of the inclusions and the difference in the
manufacturing process, the composition of metals and
dielectric materials exhibits different structural proper-
ties
[1,4]
. EMT provides many applications in material com-
posites, such as to describe anistropic media
[5,6]
, optical
properties
[7–9]
, and conductivity properties
[10]
.
Recently, Pendry et al. and Leonhardt proposed the
concept of transformation optics (TO) by using the
coordinate invariance principle of Maxwell’s equation s
and the method of coordinate transformations in math-
ematics
[4,11,12]
. Combining TO with EMT, we can realize
a series of transformation optical devices, such as cloak-
ing
[13,14]
, field rotators
[15–17]
, and field concentrators
[18–20]
.
Most of them are either with very complicated structures
and not able to be designed analytically/semi-analytically,
or with a layered system, and the effective material
parameters are limited. In this article, we will explore
anisotropic checkboard structures (CSs), which will pro-
vide an alternative choice for future TO designs.
In the past two decades, there has been a strong revival
of interest in checkboard problems focused mostly on
conductivity
[21]
and effective permittivity
[22–24]
. Various
classical mixing rules and matrix methods are proposed
to estimate the characteristics of mixtures, and they are
often used beyond their area of applicability. In this work,
we discretize two kinds of materials with unequal permit-
tivities into unit cells and arrange them in a staggered lay-
out as a checkboard-like structure. Based on EMT, we use
the band theory of the structure to get an empirical for-
mula of effective permittivities for different directions.
From numerical simulations, we demonstrate that the
EMT for the CSs is valid for unit cells in squares, rectan-
gles, and sectors in the same framework for various
material parameters.
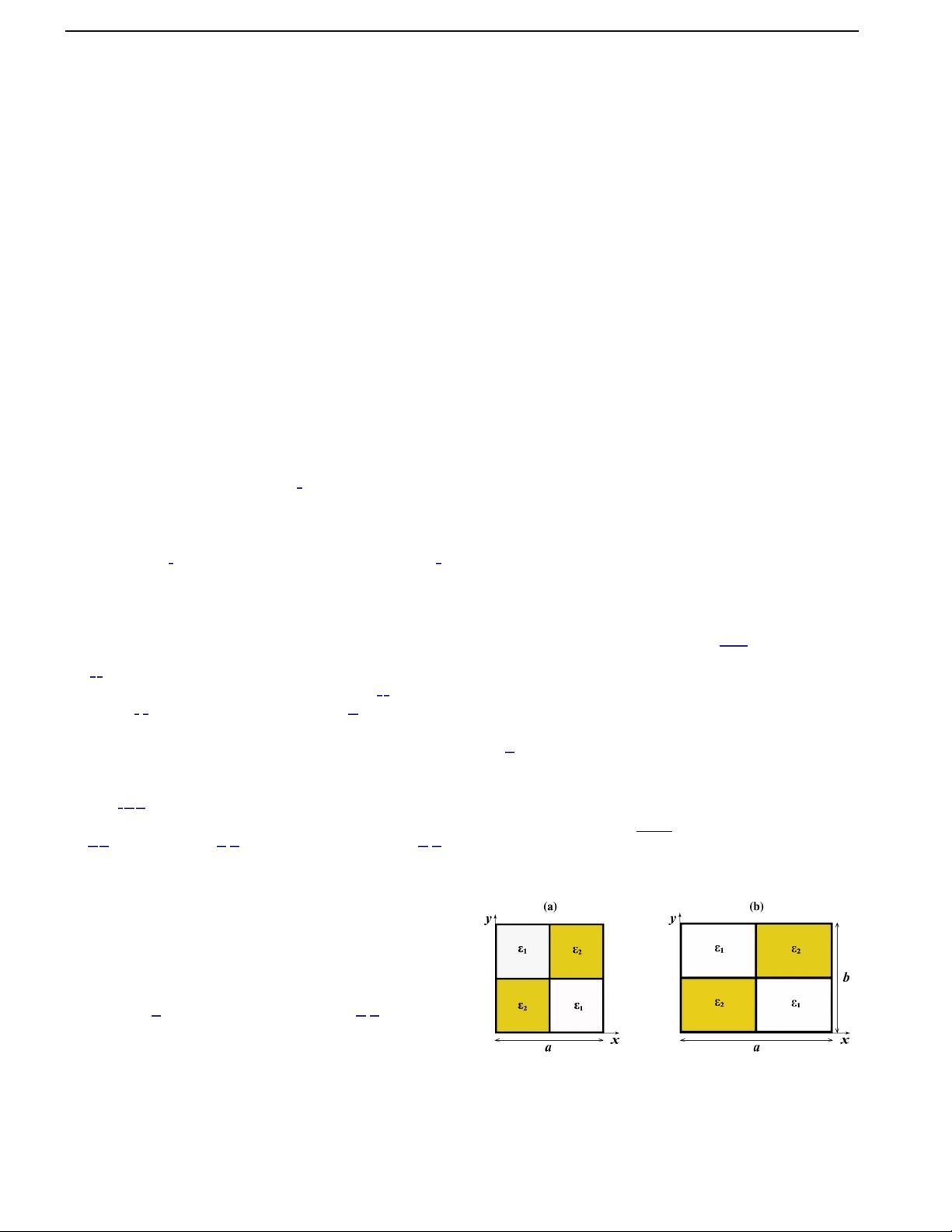
Let us start from a two-dimensional CS, which is com-
posed of alternately arranged small squares along the x
and y directions, as shown in Fig.
1(a), for a unit cell.
The lattice period is a, while the two isotropic materials
have permittivity ϵ
1
(the white square) and ϵ
2
(the yellow
square), respectively. It is easy to derive the effective
medium of such a periodic checkboard composite, which
is expected to be isotropic due to the symmetric struc-
ture
[21]
. Considering the transverse electric (TE) modes
(E
x
, E
y
, H
z
) without external electric current and charge,
the equations of electrostatics are ∇·D ¼ 0, ∇ × E ¼ 0,
and D ¼ ϵE. Defining another set of vectors D
∗
¼
ϵ
1
·ϵ
2
p
e
z
× E and E
∗
¼
1
ϵ
1
·ϵ
2
p
e
z
× D, we see that they also
satisfy the above equations:
Fig. 1. (a) Square CS with a period a. (b) Rectangular CS with a
period a along the x direction and a period b along the y direc-
tion. The permittivity of the yellow region and white region is ϵ
1
and ϵ
2
, respectively.
COL 18(7), 072401(2020) CHINESE OPTICS LETTERS July 2020
1671-7694/2020/072401(4) 072401-1 © 2020 Chinese Optics Letters









