Xilinx FPGA中的CORDIC算法实现
"Xilinx CORDIC算法用于在FPGA中执行三角函数和相关数学运算的迭代算法"
CORDIC( Coordinate Rotation Digital Computer,坐标旋转数字计算机)算法是一种在硬件中高效实现三角函数、对数和除法等数学运算的方法。Xilinx CORDIC算法是专为FPGA(Field-Programmable Gate Array,现场可编程门阵列)设计的,利用FPGA内部的乘法器和加法器资源,以迭代的方式进行计算,从而节省硬件资源和提高计算速度。
4.1 算法原理
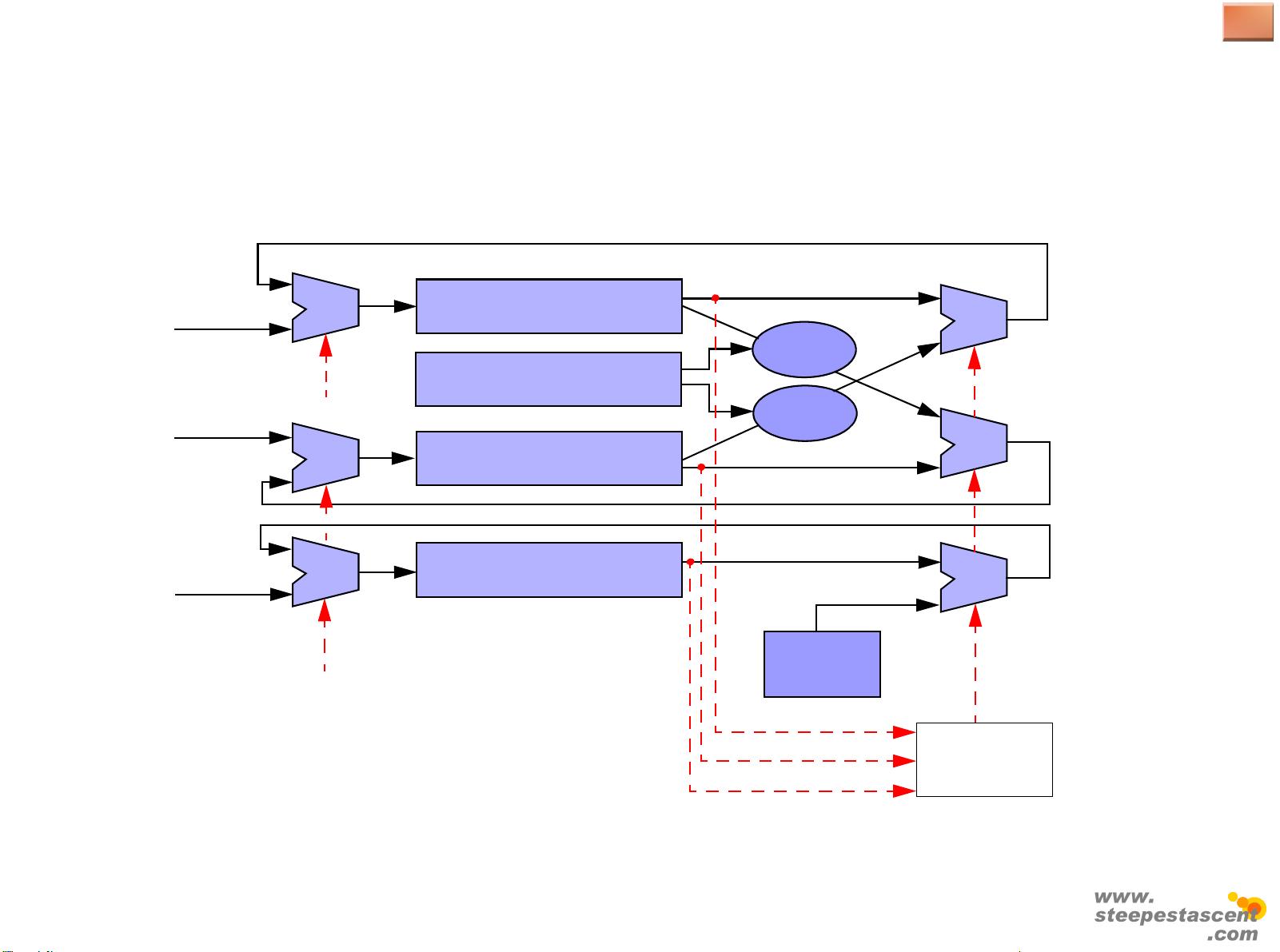
CORDIC算法基于极坐标变换,通过一系列角度的微小旋转来逼近目标函数值。它主要由以下几个步骤组成:
1. 初始化:设置初始向量(x, y)和角度θ为零。
2. 循环迭代:每次迭代都通过对x和y进行位移(左移或右移)以及更新角度θ来逼近目标值。位移的数量取决于当前迭代的步长,步长随着迭代次数的增加而减小。
3. 反转标志:根据目标函数的性质(如正弦、余弦或正切),决定是正向旋转还是反向旋转。
4. 终止条件:当达到预设的迭代次数或者误差在可接受范围内时,停止迭代。
4.2 应用场景
- 三角函数计算:例如正弦、余弦和正切。
- 平方根和除法:通过适当调整算法,可以实现对数值的平方根计算,同时也可用于除法操作。
- 对数函数:通过与指数函数的相互关系,可以间接计算对数。
4.3 历史背景
CORDIC算法由Jack Volder在1957年提出,当时由于硬件限制,移位加法是执行此类计算的可行方法。在20世纪70年代,随着手持计算器的出现,CORDIC因其高效和节省硬件资源的特性,被广泛应用于计算器中的三角函数计算。
4.4 参考资料
了解CORDIC算法的更多细节,可以参考以下资料:
1. R. Andraka. A survey of CORDIC algorithms for FPGA-based computers. www.andraka.com/cordic.htm
2. The CORDIC Algorithms. www.ee.byu.edu/ee/class/ee621/Lectures/L22.PDF
3. CORDIC Tutorial. http://my.execpc.com/~geezer/embed/cordic.htm
4. M.J. Irwin. Computer Arithmetic. http://www.cse.psu.edu/~cg575/lectures/cse575-cordic.pdf
Xilinx CORDIC算法是FPGA设计中不可或缺的一部分,它提供了在硬件中高效实现复杂数学运算的方法,尤其适合于实时和嵌入式系统应用。通过理解和掌握CORDIC算法,工程师能够优化其FPGA设计,提高性能并降低成本。
216 浏览量
376 浏览量
点击了解资源详情
点击了解资源详情
453 浏览量
5493 浏览量
huojianues
- 粉丝: 0
最新资源
- Tailwind CSS多列实用插件:无需配置的快速多列布局解决方案
- C#与SQL打造高效学生成绩管理解决方案
- WPF中绘制非动态箭头线的代码实现
- asmCrashReport:为MinGW 32和macOS构建实现堆栈跟踪捕获
- 掌握Google发布商代码(GPT):实用代码示例解析
- 实现Zsh语法高亮功能,媲美Fishshell体验
- HDDREG最终版:DOS启动修复硬盘坏道利器
- 提升Android WebView性能:集成TBS X5内核应对H5活动界面问题
- VB银行代扣代发系统源码及毕设资源包
- Svelte 3结合POI和Prettier打造高效Web开发起动器
- Windows 7下VS2008试用版升级至正式版的补丁程序
- 51单片机交通灯系统完整设计资料
- 兼容各大浏览器的jquery弹出登录窗口插件
- 探索CCD总线:CCDBusTransceiver开发板不依赖CDP68HC68S1芯片
- Linux下的VimdiffGit合并工具改进版
- 详解SHA1数字签名算法的实现过程