模糊聚类分析原理与MATLAB实现入门

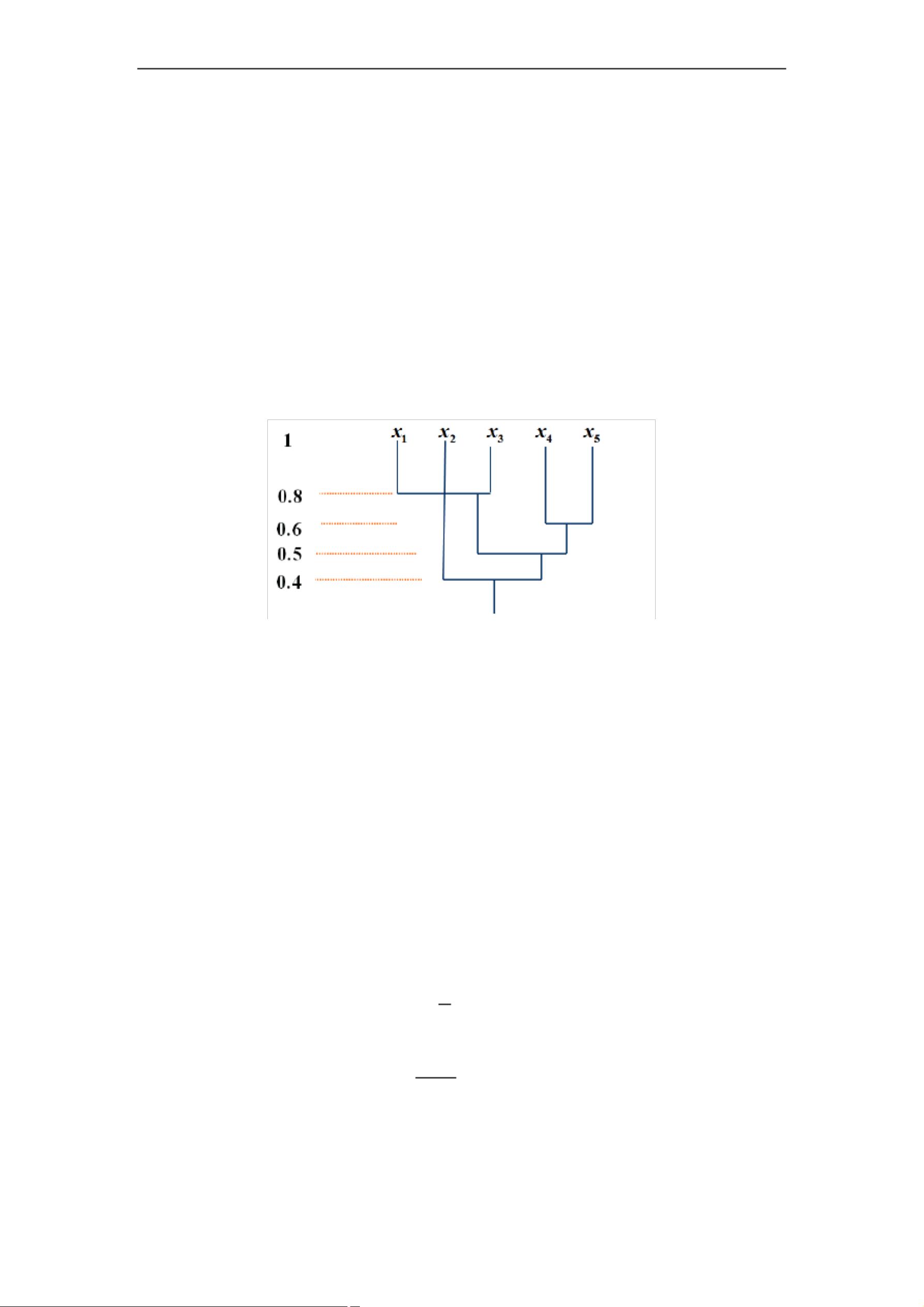
**Matlab记录文本：模糊聚类分析基础与实现** 模糊聚类分析是一种基于模糊理论的非硬划分方法，旨在更客观地反映现实世界中的样本不确定性。相比于传统硬划分的聚类分析，模糊聚类允许样本对象部分属于多个类别，这在数据量较大或类别边界模糊的情况下尤为适用。 **预备知识概要** 1. **模糊等价矩阵**：定义为满足自反性（rii=1）、对称性和传递性的矩阵R，其中传递性意味着R的幂次可以递减到一个传递闭包矩阵Rk，代表了关系的最终稳定状态。通过λ-截矩阵，模糊等价矩阵可转化为布尔矩阵，便于进行分类。 2. **λ-截矩阵操作**：对模糊矩阵A，λ-截矩阵Aλ通过阈值λ定义元素的取值，当λ增大，分类变得更细；反之，λ减小则分类变粗。例如，通过在例1中观察λ从1递减到0时的分类演变，可以理解模糊等价关系如何随λ的变化动态调整。 **模糊聚类算法介绍** 文章首先介绍了两种适合小型数据集且有助于理解模糊聚类原理的方法： - **基于择近原则的模糊聚类**：这种方法根据样本间的相似度进行聚类，允许样本点部分归属不同类别，增强了聚类结果的灵活性。 - **基于模糊等价关系的聚类**：利用模糊等价矩阵构建的分类系统，能够捕捉样本间的中间地带，反映样本的模糊属性。 在Matlab中实现模糊聚类分析，可能涉及以下步骤： - **构建模糊相似矩阵**：通过计算样本间的相似度度量，如欧几里得距离或皮尔逊相关系数，构造模糊相似矩阵。 - **构造λ-截矩阵**：选择合适的λ值，对模糊相似矩阵进行剪裁，得到布尔等价矩阵。 - **迭代计算**：通过计算矩阵的幂次或执行模糊C均值（Fuzzy C-Means, FCM）算法，直到达到收敛条件，得到模糊聚类结果。 - **解读和可视化**：分析λ的变化对聚类结果的影响，绘制聚类树或热力图，展示样本的模糊归属。 这篇文档详细探讨了模糊聚类分析的基本原理、矩阵操作以及在Matlab中的实际应用，适合对模糊聚类感兴趣或者需要在数据分析中处理模糊信息的读者参考。