压缩感知下隐私保护的同态外包图像多对一加密技术

95 浏览量更新于2024-08-26 收藏 3.37MB PDF 举报

本文主要探讨了一种结合了压缩感知（Compressive Sensing, CS）理论与隐私保护、同态外包解密技术的创新一对多图像加密方案。在数字信号处理领域（Digital Signal Processing, DSP）的最新研究中，发表于2019年第95期的《Digital Signal Processing》期刊上，该研究论文的题目为“基于压缩感知的具有隐私保护的同态外包解密的一对多图像加密”（One-to-many image encryption with privacy-preserving homomorphic outsourced decryption based on compressive sensing）。压缩感知是一种信号处理方法，它允许在采样阶段直接从原始信号中提取出关键信息，而无需进行传统的密集采样。这在图像处理、无线通信、医学成像和光学等领域取得了显著的进步。作者团队由Dong Xie、Fulong Chen、Yonglong Luo和Lixiang Li等来自安徽师范大学计算机与信息学院、北京邮电大学网络与交换技术国家重点实验室以及安徽省网络安全与信息技术重点实验室的研究人员组成。文章的核心内容聚焦在如何利用CS原理实现一对多图像加密，即一个密钥可以同时加密多个图像，但每个接收者只能解密其对应的特定图像。这种方法旨在提供更高的效率，因为单次操作可以处理多个数据，同时保持信息安全。隐私保护是另一个关键要素，通过设计特殊的加密算法，确保即使在外部服务提供商处进行解密，数据也无法被非授权方轻易获取或解析。此外，文中还可能讨论了如何将同态加密（Homomorphic Encryption）的概念融入其中。同态加密允许在不解密数据的情况下执行计算，这对于云计算环境中的数据处理非常有用，因为它允许在不暴露原始数据的情况下进行运算，提高了数据处理的灵活性和安全性。文章历史显示，该研究在2019年9月27日在线发布，关键词包括压缩感知、一对多加密、隐私保护和同态外包解密，这些关键词揭示了研究的核心技术和应用背景。总体来说，这篇论文深入探讨了将压缩感知技术应用于图像加密领域的前沿实践，对于信息安全、云计算和大数据处理的隐私保护策略具有重要意义。

D. Xie et al. / Digital Signal Processing 95 (2019) 102587 3

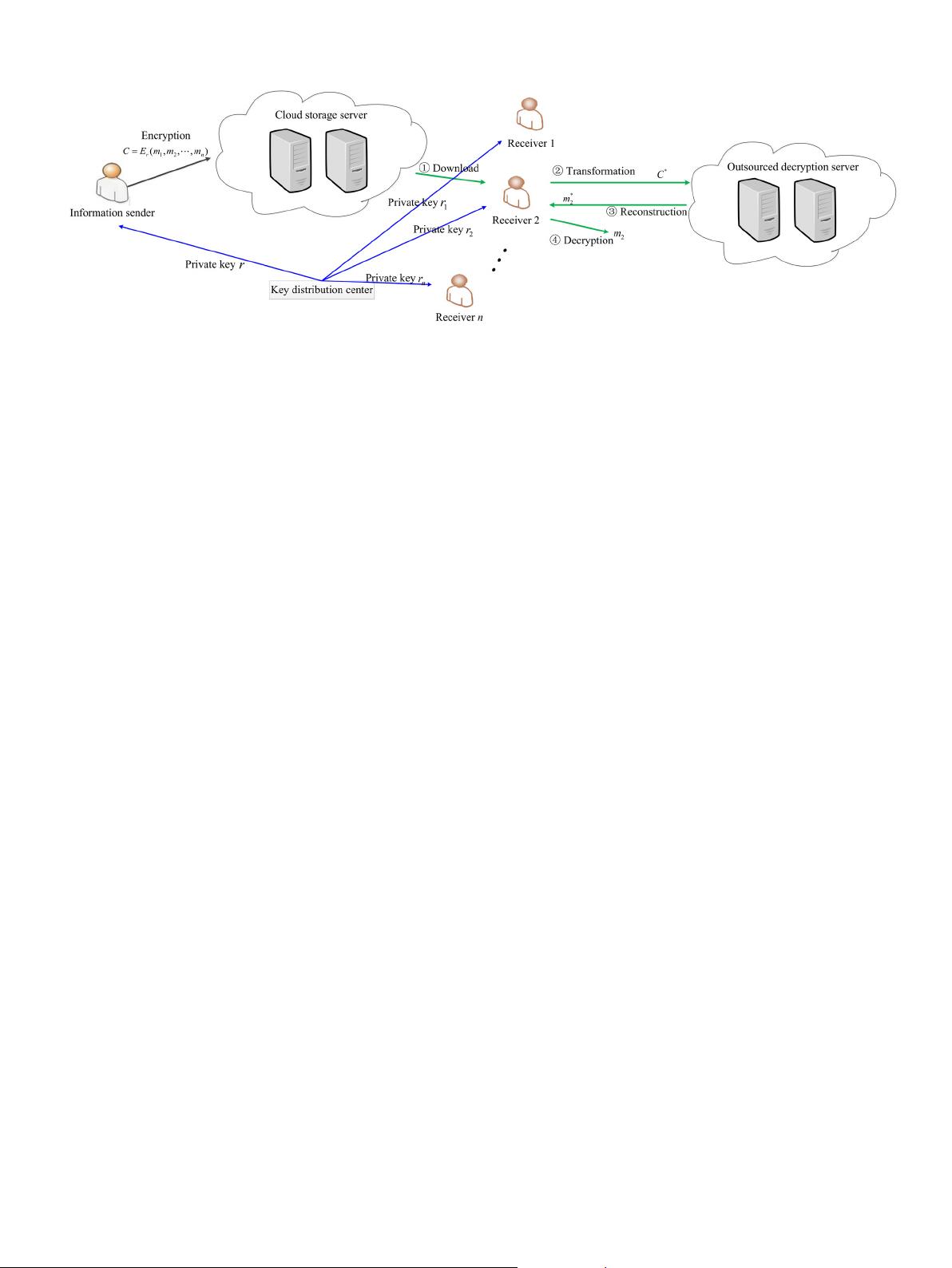
Fig. 3. The framework of the proposed scheme.

requirements of decryption algorithms. Thus, the eﬃciency is one

of the major obstacles to applying this encryption framework to a

resource-constrained embedded application scenarios.

this paper, we present aone-to-many encryption method

with the privacy-preserving homomorphic outsourced decryption

based on CS. Fig. 3 shows the schematic diagram of the proposed

framework. The main contribution of this work can be summarized

as follows:

• First, we present a novel attribute-based key distribution

mechanism for the proposed symmetric cryptosystem. In tra-

ditional

symmetric encryption schemes, each user should store

n − 1private keys and the number of keys are C

, where n

the number of users. Our scheme employs the social at-

tributes

of each user. We formalize these social attributes of

each user according to certain partitioning rules, and these at-

tributes

form the attribute set of this user. Thus, all attributes

of n users form the maximum attribute set MAS. The trusted

key distribution center (KDC) distributes private keys for each

user according to the attribute set of this user. Thus, the pri-

vate

key storage space of each user is equal to the size of its

attribute set, and the number of the total keys is |MAS |.

• Second, we break through the traditional one-to-one CS-based

encryption method, and introduce aone-to-many encryption

framework according to the proposed attribute-based key dis-

tribution

mechanism. In our scheme, the sender can encrypt

multiple plaintexts for different users simultaneously accord-

ing

to the attributes he owns. If a user has one or more

attributes which the sender uses for encryption, then he can

decrypt the corresponding plaintexts from the ciphertexts.

• Last, the receiver does not decrypt each acquired ciphertext

himself, but outsources the decryption process to an un-

trusted

third party cloud server, called Outsourced Decryption

Server (ODS). The purpose of doing this is to improve the

eﬃciency of the decryption process. Note that CS-based en-

cryption

schemes are not applicable for resource-constrained

embedded systems, especially for high-dimensional image de-

cryptions.

To protect the secrecy of plaintexts, we introduce

a transformation algorithm which can transform the original

decryption problem into a variant one. The receiver does not

send the original decryption problem directly to the ODS, but

sends a variant one. Thus, the ODS does not obtain the original

plaintexts after performing the decryption process.

1.1. Organization

The rest of this paper is organized as follows. Section 2 recalls

some basic background of chaotic maps and the CS theory. We

will introduce the proposed one-to-many encryption scheme ex-

plicitly

in Section 3. Section 4 gives the security analysis about our

scheme. In Section 5, some experiments are carried out to show

the feasibility and the superiority of the proposed scheme. Finally

we conclude this paper in Section 6.

2. Background

2.1. Chaotic maps

Here we give the simple deﬁnitions of three kinds of chaotic

maps, which are used for constructing chaotic measurement ma-

trices

in our experiments.

2.1.1.

Logistic map

The

standard logistic map is deﬁned recurrently by

x(n +1) = 4x(n)(1 − x(n)), (1)

where x(0) ∈ (0, 1) is the initial value and thus x(n) ∈ (0, 1).

2.1.2.

Skew tent map

The

one-dimensional skew tent map with parameter μ is given

y(n + 1) =



y(n)/μ 0 < y(n)<μ

1 − y(n)/(1 −μ) μ ≤ y(n)<1

, (2)

where y(0) ∈ (0, 1) is the initial value and μ ∈ (0, 1) is a system

parameter.

2.1.3.

Chebyshev map

The

w-th order Chebyshev map is deﬁned by

z(n + 1) = cos(w arccos(z(n))), (3)

where this map is chaotic for w ≥2, and z(n) ∈ (−1, 1).

2.2. Compressed sensing

To compress an n-dimensional sparse vector x, the compression

process of CS can be represented by a special case of the underde-

termined

linear system:

y =Ax, (4)

where A ∈ R

m×n

(m < n) and y ∈ R

denote the measurement

matrix and the measurement vector, respectively. Here we call a

vector x k-sparse if it has at most k nonzero entries. Similarly, the

sparsity of a matrix X is the maximum number of nonzero entries

of column vectors in X. Previous studies show that some natural

signals can be represented using only a few non-zero coeﬃcients

剩余13页未读，继续阅读

weixin_38592332

粉丝: 7
资源: 888

压缩感知下隐私保护的同态外包图像多对一加密技术

压缩感知非常好的源代码

基于同态加密的DBSCAN聚类隐私保护方案.docx

工厂线校准与压缩感知：同态外包解密的隐私保护图像加密

通过有效验证来保护隐私的同态MAC

同态加密技术及其在云计算隐私保护中的应用.pdf

具有小CiphertextExpandsion的图像同态加密方案的仅Ciphertext-Only攻击

同态加密是什么-以及学习同态加密的意义

基于同态加密的高效多方保密计算

压缩公钥的快速全同态加密方案

云外包多方隐私集合比较：同态加密与Bloom过滤器结合的新协议

最新资源