C++最佳实践：二叉搜索树详解

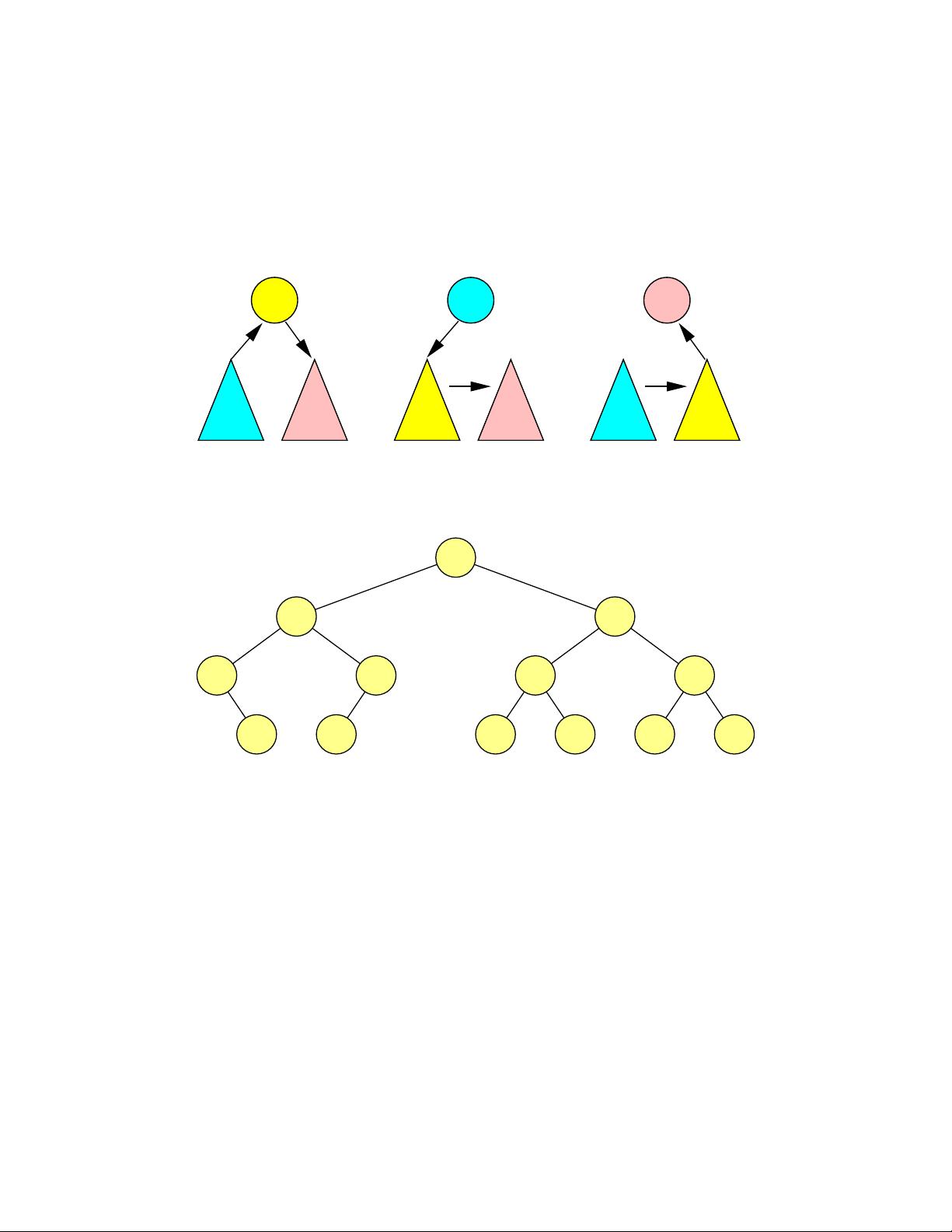
"C++最佳实践——二叉搜索树" 在C++编程中，遵循最佳实践是提高代码质量、可读性和效率的关键。二叉搜索树（Binary Search Tree, BST）是一种特殊的二叉树，其每个节点都具有BST属性：对于任意两个节点x和y，如果y是x的左子树中的节点，那么y的键值小于x的键值；如果y是x的右子树中的节点，那么y的键值大于x的键值。这里假设BST中的键值都是唯一的。 每个BST节点通常包含以下属性： 1. `p`：指向父节点的指针。 2. `left`：指向左孩子的指针。 3. `right`：指向右孩子的指针。 4. `key`：存储在节点上的键值。 例如，下面是一个BST的示意图： ``` 4 / \ 2 6 / \ / \ 3 5 9 12 / \ / \ / \ 1 2 8 11 15 20 ``` 在BST中，有三种主要的遍历策略，它们决定了访问节点的顺序： 1. **中序遍历（Inorder Traversal）**：首先访问左子树，然后访问当前节点，最后访问右子树。对于BST，中序遍历会按照键值的升序输出节点。 2. **前序遍历（Preorder Traversal）**：先访问当前节点，然后是左子树，最后是右子树。这种遍历方式常用于复制整棵树或打印树的结构。 3. **后序遍历（Postorder Traversal）**：先访问左子树，然后是右子树，最后访问当前节点。后序遍历在计算节点的总和或释放树的所有节点时很有用。 在C++中实现这些遍历策略，通常会使用递归方法。例如，对于中序遍历，可以使用以下伪代码： ```cpp void inorderTraversal(Node* node) { if (node != nullptr) { inorderTraversal(node->left); // 访问当前节点 visit(node->key); inorderTraversal(node->right); } } ``` 为了确保C++代码的最佳实践，还需要注意其他方面，比如内存管理（使用智能指针避免内存泄漏）、错误处理（使用异常处理机制）、代码风格（遵循统一的编码规范）以及算法效率（优化查找、插入和删除操作）。理解并熟练应用这些概念，可以帮助开发者编写出高效且易于维护的C++代码。