1800 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 45, NO. 7, JULY 1997
ML Estimation of Time and
Frequency Offset in OFDM Systems
Jan-Jaap van de Beek, Student Member, IEEE, Magnus Sandell, Student Member, IEEE,
and Per Ola B¨orjesson,
Member, IEEE
Abstract— We present the joint maximum likelihood (ML)
symbol-time and carrier-frequency offset estimator in orthogo-
nal frequency-division multiplexing (OFDM) systems. Redundant
information contained within the cyclic prefix enables this es-
timation without additional pilots. Simulations show that the
frequency estimator may be used in a tracking mode and the
time estimator in an acquisition mode.
I. INTRODUCTION
O
RTHOGONAL frequency-division multiplexing
(OFDM) systems have recently gained increased
interest. OFDM is used in the European digital broadcast
radio system and is being investigated for other wireless
applications such as digital broadcast television and mobile
communication systems, as well as for broadband digital
communication on existing copper networks. See [1] and [2]
and the references therein.
We address two problems in the design of OFDM receivers.
One problem is the unknown OFDM symbol arrival time.
Sensitivity to a time offset is higher in multicarrier systems
than in single-carrier systems and has been discussed in [3]
and [4]. A second problem is the mismatch of the oscillators
in the transmitter and the receiver. The demodulation of a
signal with an offset in the carrier frequency can cause a high
bit error rate and may degrade the performance of a symbol
synchronizer [3], [5].
A symbol clock and a frequency offset estimate may be
generated at the receiver with the aid of pilot symbols known
to the receiver [6], [7], or, as in [8], by maximizing the
average log-likelihood function. Redundancy in the transmitted
OFDM signal also offers the opportunity for synchronization.
Such an approach is found in [7], [9], and [10] for a time
offset and in [10]–[12] for a frequency offset. We present
and evaluate the joint maximum likelihood (ML) estimation
of the time and carrier-frequency offset in OFDM systems.
The key element that will rule the discussion is that the OFDM
data symbols already contain sufficient information to perform
synchronization. Our novel algorithm exploits the cyclic prefix
preceding the OFDM symbols, thus reducing the need for
pilots.
Manuscript received December 1, 1996; revised January 2, 1997. The
associate editor coordinating the review of this paper and approving it for
publication was Prof. Giorgios B. Giannakis.
The authors are with the Division of Signal Processing and the Centre
for Distance–Spanning Technology, Lule
˚
a University of Technology, Lule
˚
a,
Sweden.
Publisher Item Identifier S 1053-587X(97)04946-5.
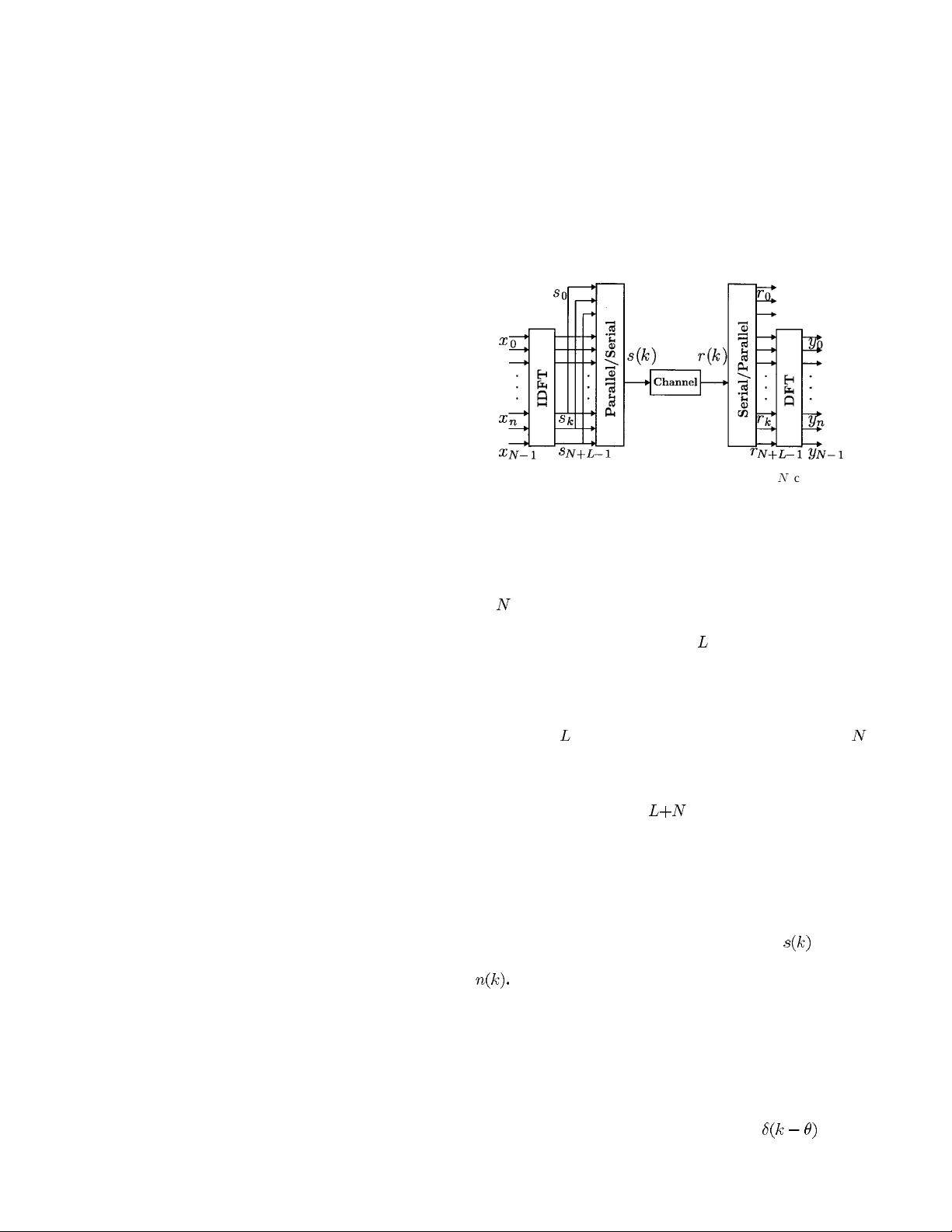
Fig. 1. OFDM system, transmitting subsequent blocks of
N
complex data.
II. THE OFDM SYSTEM MODEL
Fig. 1 illustrates the baseband, discrete-time OFDM system
model we investigate. The complex data symbols are modu-
lated by means of an inverse discrete Fourier transform (IDFT)
on
-parallel subcarriers. The resulting OFDM symbol is se-
rially transmitted over a discrete-time channel, whose impulse
response we assume is shorter than
samples. At the receiver,
the data are retrieved by means of a discrete Fourier transform
(DFT).
An accepted means of avoiding intersymbol interference
(ISI) and preserving orthogonality between subcarriers is to
copy the last
samples of the body of the OFDM symbol (
samples long) and append them as a preamble—the cyclic
prefix—to form the complete OFDM symbol [1], [2]. The
effective length of the OFDM symbol as transmitted is this
cyclic prefix plus the body (
samples long). The insertion
of a cyclic prefix can be shown to result in an equivalent
parallel orthogonal channel structure that allows for simple
channel estimation and equalization [13]. In spite of the loss of
transmission power and bandwidth associated with the cyclic
prefix, these properties generally motivate its use [1], [2].
In the following analysis, we assume that the channel is
nondispersive and that the transmitted signal
is only
affected by complex additive white Gaussian noise (AWGN)
We will, however, evaluate our estimator’s performance
for both the AWGN channel and a time-dispersive channel.
Consider two uncertainties in the receiver of this OFDM
symbol: the uncertainty in the arrival time of the OFDM
symbol (such ambiguity gives rise to a rotation of the data
symbols) and the uncertainty in carrier frequency (a difference
in the local oscillators in the transmitter and receiver gives rise
to a shift of all the subcarriers). The first uncertainty is modeled
as a delay in the channel impulse response
, where
1053–587X/97$10.00 1997 IEEE









