HHT技术探讨：希尔伯特边际谱与瞬时频率分析

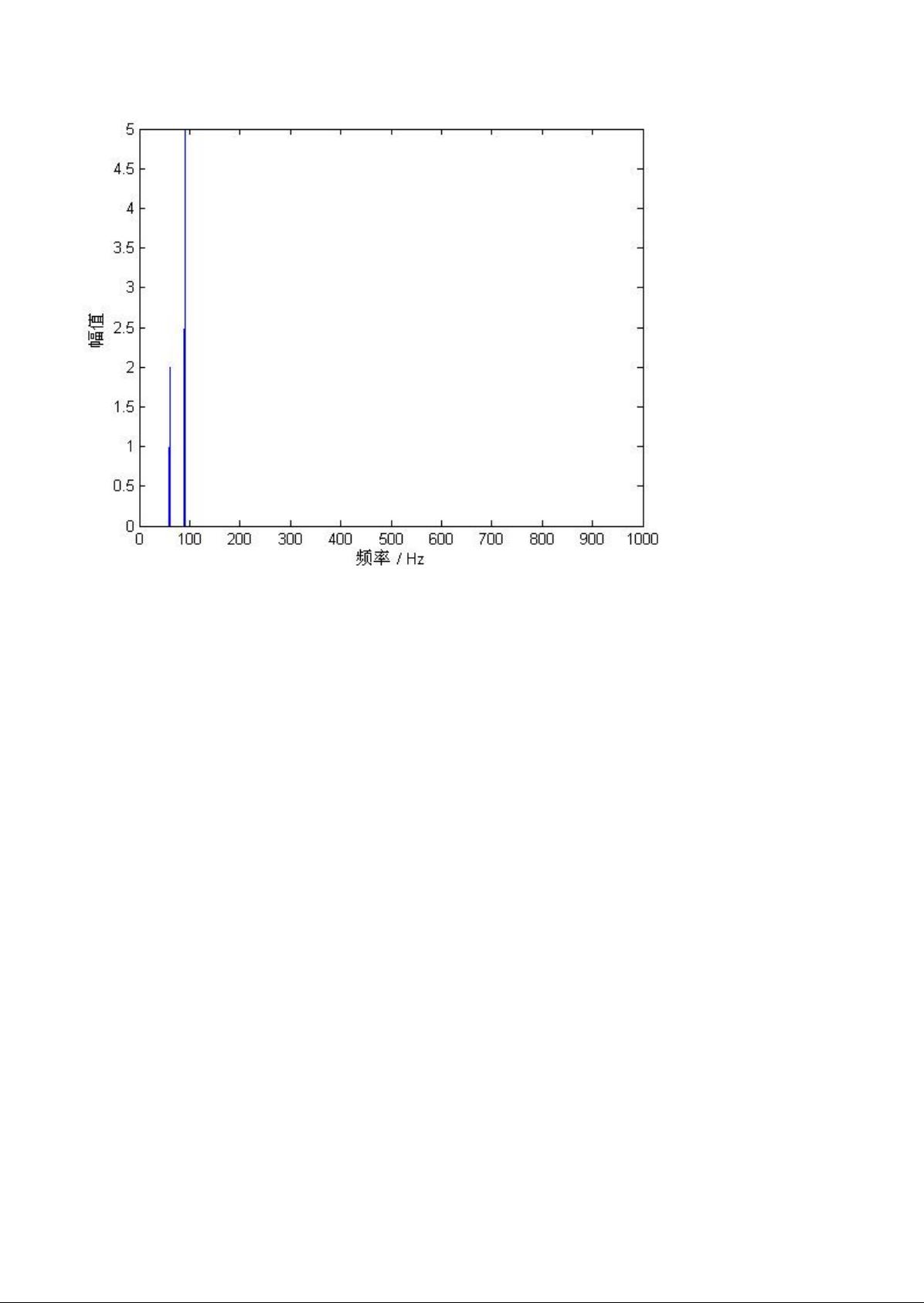
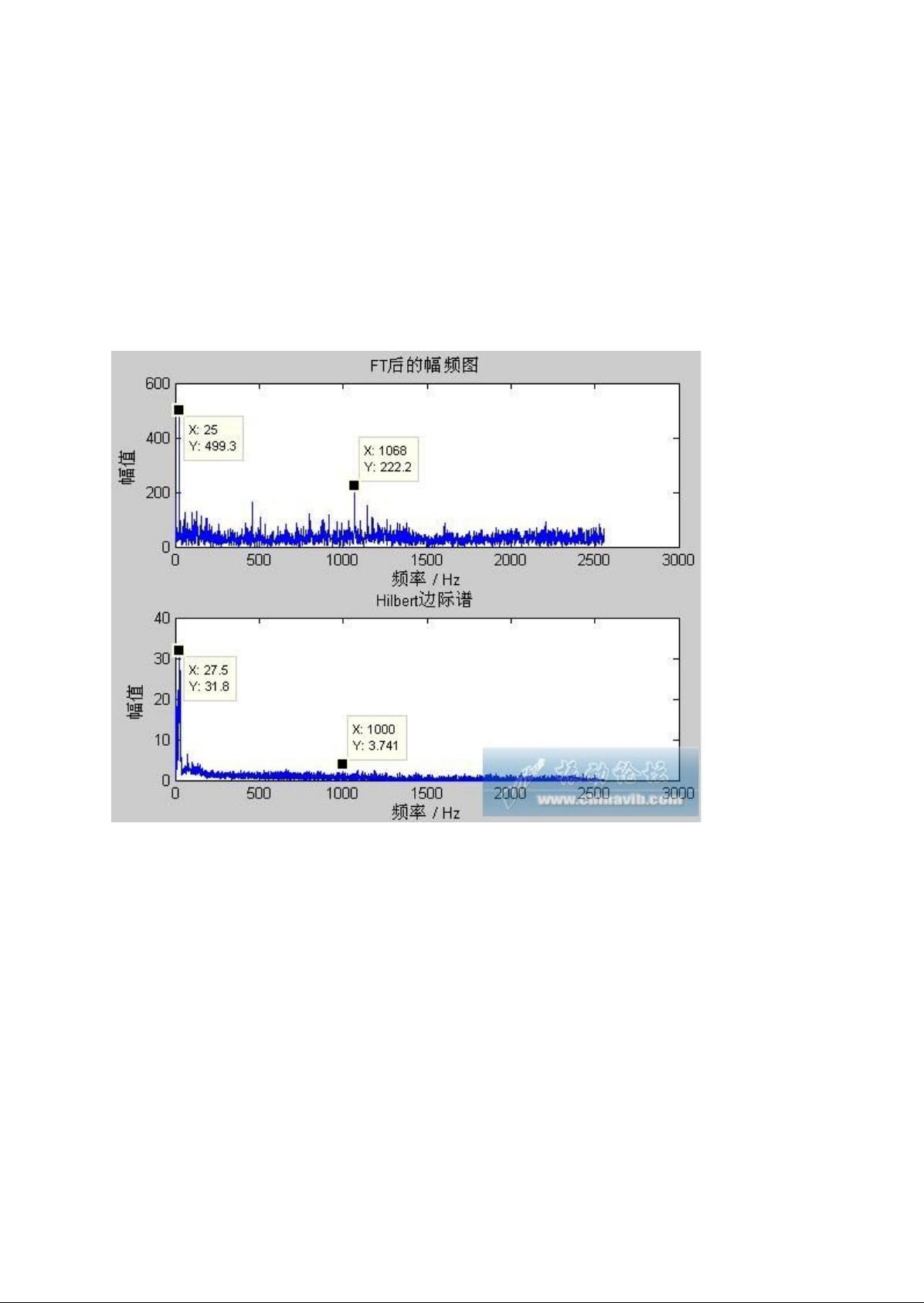
"HHT问题讨论，涉及希尔伯特边际谱、瞬时频率计算、EMD分解、HHT应用以及相关代码实现与问题讨论" 希尔伯特-汉明变换（Hilbert-Huang Transform，简称HHT）是一种时频分析方法，主要用于非线性、非平稳信号的分析。在HHT中，希尔伯特边际谱（Hilbert Marginal Spectrum）是一个关键概念，它是通过希尔伯特变换得到的瞬时频率和幅度的乘积进行积分得到的，能够提供信号的瞬时功率信息。希尔伯特变换能够将信号转换为它的瞬时相位和幅度，而边际谱则是在频域上对这些瞬时幅度进行积分，从而获得信号在整个频率范围内的能量分布。 HHT的另一个组成部分是经验模态分解（Empirical Mode Decomposition，简称EMD），它是一种自适应的数据分解方法，能将复杂信号分解为一系列内在模态函数（Intrinsic Mode Function，简称IMF）。EMD通过对信号进行迭代的局部平均和峰值提取过程来实现，每一步都生成一个新的IMF，直到剩余部分仅剩下趋势项。 在HHT的实际应用中，EEMD（Ensemble Empirical Mode Decomposition）被提出以解决EMD的噪声敏感性和随机性问题，通过多次分解并取平均来提高稳定性。然而，EEMD的使用也会带来一些问题，例如如何选择合适的噪声嵌入量和如何避免过分解。 求取瞬时频率时，可能会遇到instfreq函数使用上的困难。instfreq函数用于计算每个IMF的瞬时频率，但其结果可能受到数据质量、采样率等因素的影响。对于调频信号，HHT和傅里叶变换（FFT）都有各自的适用场景，FFT适用于平稳信号，而HHT则擅长处理非平稳信号，因此选择哪种方法取决于信号的特性。 在MATLAB中，可以使用hhspectrum等工具箱函数来计算HHT谱和边际谱，但自定义代码可能会出现一些问题，如谱图粗糙、频率分辨率不足等。这可能需要调整参数、优化算法或者检查数据预处理步骤。 HHT时频灰度谱可以转换为黑白谱以提高视觉效果，这通常涉及到对灰度值的阈值处理。HHT谱图的异常可能是由于计算错误、数据噪声或者参数设置不当引起的，需要仔细检查计算流程和输入数据。 三维HHT图可以提供更丰富的信息，包括时间、频率和幅度三个维度，有助于深入理解信号的动态特性。 HHT是一种强大的信号分析工具，但其应用需要深入理解和掌握相关理论，并且在实践中不断调试和优化算法以适应各种复杂信号。对于初学者或研究者来说，参与讨论、分享经验和学习相关资源是提高HHT应用能力的有效途径。