排序二叉树的理解与维护

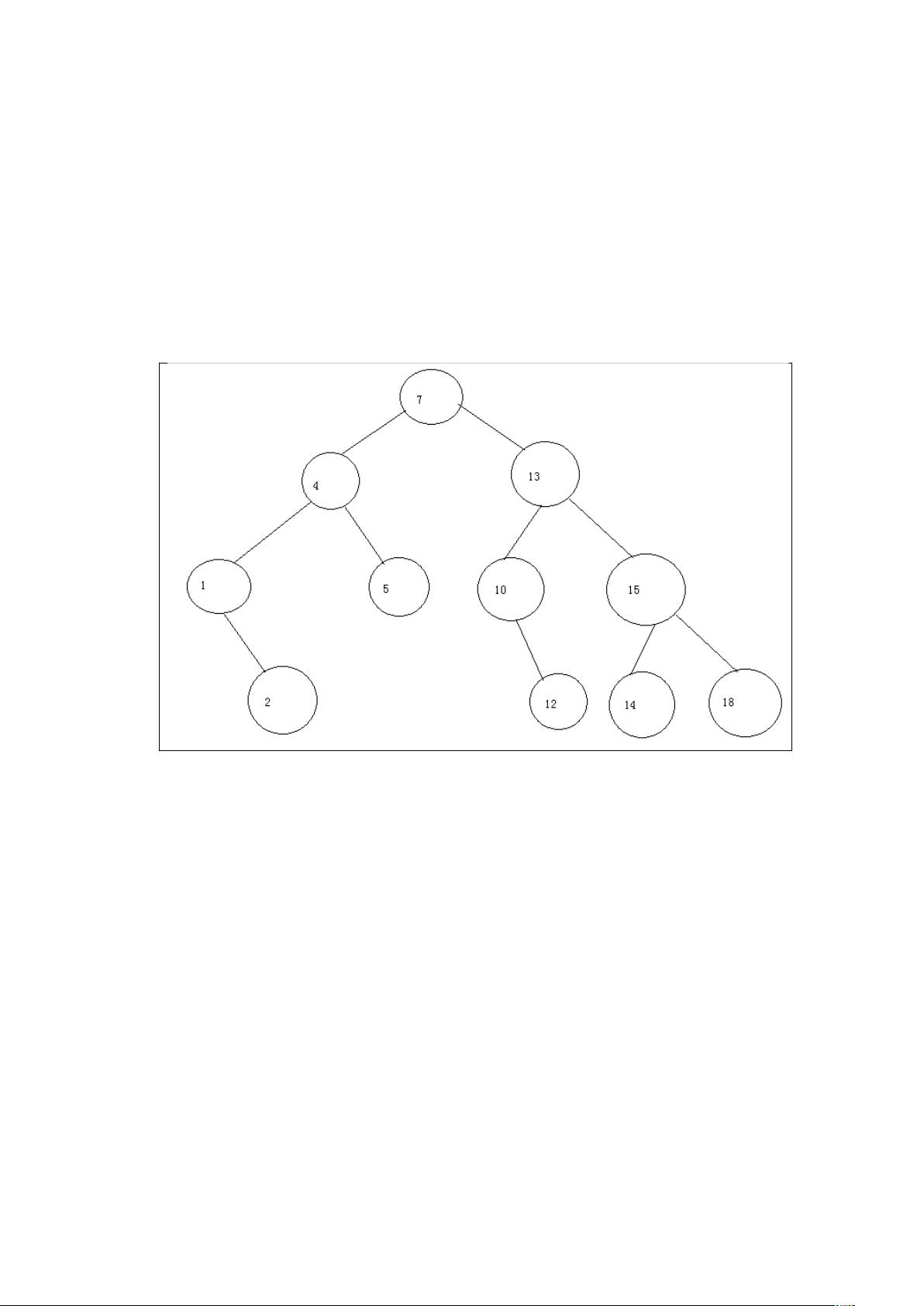
"Java基础复习笔记10数据结构-排序二叉树" 排序二叉树是一种特殊类型的二叉树，其每个节点的值都大于其左子树中的所有节点值，且小于或等于其右子树的所有节点值。这种结构使得在排序二叉树上进行查找、插入和删除操作具有较高的效率，特别是对于有序数据的操作。 1. 排序二叉树的特性 - 所有节点的数据都有可比较性。 - 根节点的值大于左子树所有节点的值。 - 根节点的值小于或等于右子树所有节点的值。 - 左子树中的每个节点的值小于其父节点的值。 - 右子树中的每个节点的值大于或等于其父节点的值。 2. 使用场景 - 快速排序：由于排序二叉树的特性，可以方便地通过中序遍历得到有序序列，适合快速排序。 - 查找操作：查找特定值的节点效率较高，时间复杂度可以达到O(log n)。 3. 维护排序二叉树 - 新增节点：新增节点时，需要从根节点开始比较，根据值的大小确定节点应插入的位置，确保树的性质不被破坏。如果新节点值小于当前节点，则插入到左子树；如果新节点值大于当前节点，则插入到右子树，直到找到合适的插入位置。 - 删除节点： - 叶子节点：若被删除节点无子节点，直接删除，不影响树的结构。 - 单子树节点：若被删除节点只有一个子节点，将子节点提升到父节点的位置，替换被删除节点。 - 双子树节点：最复杂的情况，需要找到被删除节点的后继（右子树的最小节点）或前驱（左子树的最大节点），用这个节点替换被删除节点，然后删除找到的节点。若找不到这样的节点，可以采用其他方法如红黑树的平衡策略来调整。 4. 算法代码实现 - 创建排序二叉树：通常通过递归方式实现，比较新节点与当前节点的值，决定新节点的位置。 - 插入节点：按照上述规则，从根节点开始，比较新节点和当前节点的值，直到找到合适的位置。 - 删除节点：需要判断被删除节点的子节点情况，根据情况执行相应的替换或调整操作。 在实际编程中，可以定义一个`Node`类表示二叉树节点，包含数据、左子节点和右子节点属性，然后提供`insert`、`delete`等方法来实现这些操作。在Java中，可以使用面向对象的方式设计和实现这些功能。 例如： ```java class Node { int data; Node left, right; // 构造函数 Node(int item) { data = item; left = right = null; } } class BinaryTree { Node root; // 插入节点 void insert(int key) {...} // 删除节点 Node deleteNode(Node root, int key) {...} } ``` 这里仅展示了类的定义，实际的`insert`和`deleteNode`方法需要根据上述逻辑完成。 总结，排序二叉树是数据结构中一种有效的数据组织方式，它结合了二叉树和排序的特点，为查找和排序操作提供了高效的方法。理解和掌握排序二叉树的插入、删除和查找算法对于提升Java编程能力非常有帮助。