Eviews教程：多元线性回归模型检验详解

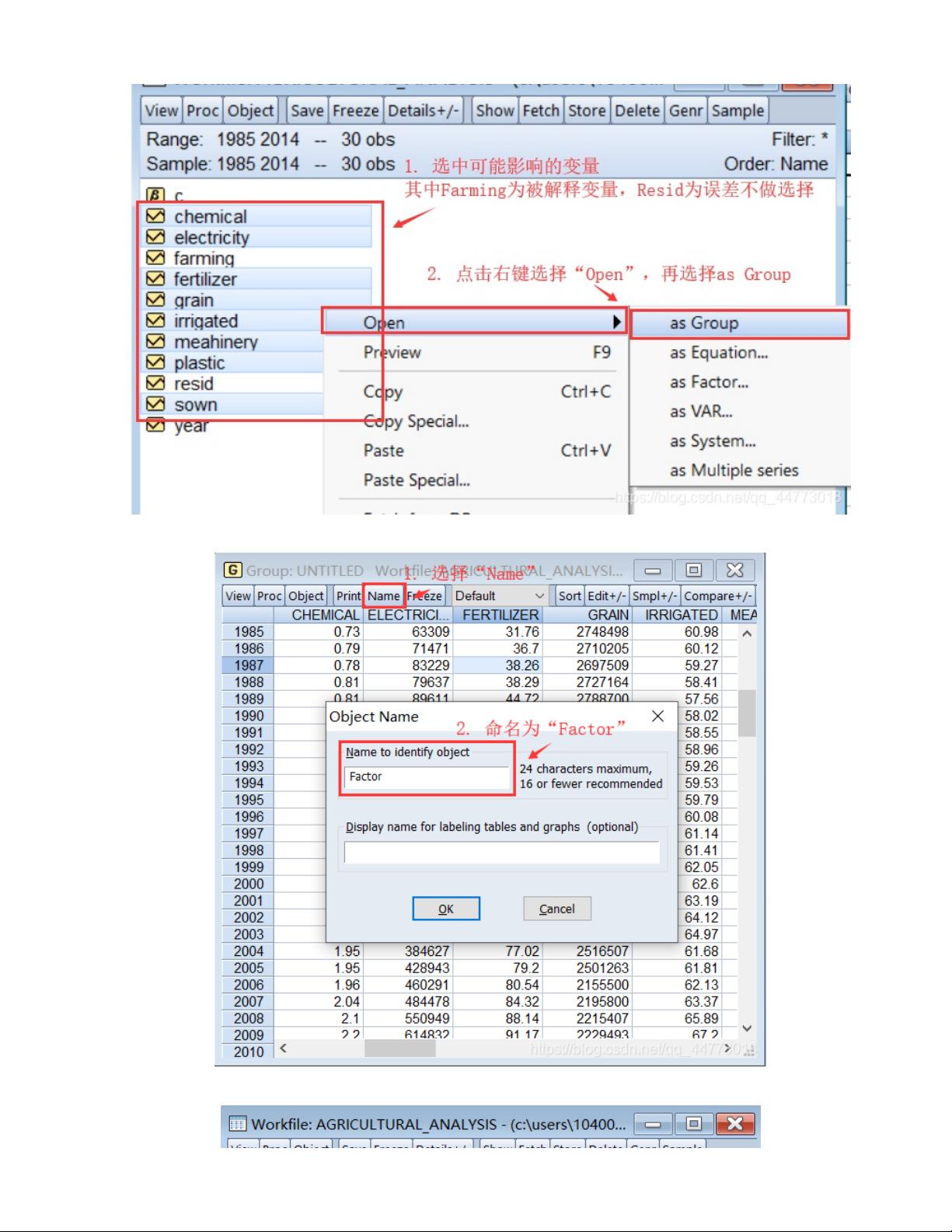
该资源是一份关于使用Eviews软件进行零基础学习的教程，专注于多元线性回归模型的常见检验，包括模型的建立、参数检验、多重共线性、正态性、异方差性和稳定性检验。 正文: 多元线性回归模型是统计学和经济学中常用的一种分析工具，用于研究多个自变量如何影响一个因变量。在这个【零基础Eviews实例】中，我们主要探讨了如何在Eviews环境下进行此类模型的构建和检验。 首先，我们需要进行前期准备工作。这包括创建一个新的工作文件，设置合适的日期范围，并导入数据。在Eviews中，可以通过“File”菜单的“New”选项创建工作文件，使用命令`wfcreatea19852014`设定时间跨度。接着，创建一个空的数据集，并通过“Quick”菜单的“EmptyGroup”导入数据。 接下来，我们要建立模型并进行参数检验。定义影响因素组，比如将所有可能影响因变量的变量放入一个名为“Factor”的组。然后，通过“Estimate Equation”或者在命令行输入`lsfarmingcfactor`来创建方程并估计模型。模型的显著性通常通过F统计量和t统计量及其对应的P值来判断。如果P值小于显著性水平（如0.05），则认为模型或系数显著。 对于多重共线性问题，这是一种当自变量之间存在高度相关性时可能出现的问题。在这种情况下，尽管模型整体可能通过F检验，但单个系数的t检验可能不显著。我们可以使用Variance Inflation Factor (VIF)进行检验，VIF值大于10通常被视为存在多重共线性风险。在Eviews中，可以通过“View”菜单的“Coefficient Diagnostics”下的“Variance Inflation Factors”来查看VIF值。 除了多重共线性，还需要检查模型的其他方面。例如，随机误差项的正态性检验可以通过残差图或者Shapiro-Wilk检验来完成，确保误差项符合正态分布假设。异方差性检验，如White检验或Breusch-Pagan检验，用来检查因变量的方差是否随自变量的变化而变化。模型结构稳定性检验，如Durbin-Watson统计量，可以帮助检测自相关性。 这个Eviews实例详细介绍了如何在实际操作中进行多元线性回归模型的建立和检验，对于初学者来说是一份非常实用的指南。它涵盖了从数据导入到模型检验的整个流程，强调了模型稳健性的重要性，对于理解回归分析的基本步骤和注意事项具有很大的帮助。通过这样的实践，用户不仅能掌握Eviews软件的使用，还能对统计模型的构建和解释有更深入的理解。