CD2FA：深度包检测的高效压缩算法
5星 · 超过95%的资源 需积分: 9 83 浏览量
更新于2024-12-02
收藏 339KB PDF 举报 "Advanced Algorithms for Fast and Scalable Deep Packet Inspection - Sailesh Kumar, Jonathan Turner, John Williams"
在网络安全领域，深度包检测（Deep Packet Inspection, DPI）是一种关键的技术，用于检查网络数据流中的特定模式，如恶意软件签名、敏感信息等。传统的DPI算法主要依赖确定性有限状态自动机（Deterministic Finite Automata, DFA）来解析正则表达式。DFA具有高效性，但当处理网络应用中复杂的模式时，可能会占用大量的内存。
DFA的表压缩技术虽能略微减少内存需求，但仍然不能解决根本问题，因为每次处理输入字符时仍需额外的内存访问。另外，非确定性有限状态自动机（NFA）和延迟输入DFA（Delayed Input DFA, D2FA）虽然在内存使用上更优，但其吞吐量却不如未压缩的DFA。
在论文"Advanced Algorithms for Fast and Scalable Deep Packet Inspection"中，作者引入了一种新的结构——内容寻址延迟输入DFA（Content-Addressed Delayed Input DFA, CD2FA）。CD2FA旨在提供一个紧凑的正则表达式表示方式，同时保持与传统未压缩DFA相当的处理速度。其创新之处在于，CD2FA通过内容来定位D2FA的连续状态，而不是使用传统的“状态编码”方法，这极大地优化了内存使用和查找效率。
CD2FA的设计考虑了内存效率和性能的平衡。通过利用内容寻址，它可以减少对内存的需求，而通过保持与DFA相当的吞吐量，它能够在大规模网络环境中实现快速的包检测。这种方法对于处理现代网络流量中的大量和复杂模式尤其有利，因为它能在不牺牲性能的前提下降低系统资源的消耗。
此外，论文可能还探讨了CD2FA与其他DPI算法的比较，包括它们在不同工作负载下的性能表现、内存占用以及扩展性。可能还包括了实证分析和实验结果，以证明CD2FA在实际环境中的优越性。这样的技术进步对于构建更加高效、可扩展的网络安全系统至关重要，特别是在面对日益增长的网络威胁和海量数据流的挑战时。
这篇论文提出的CD2FA是DPI算法的一个重要进展，它结合了内存效率和高速处理的能力，为大规模的网络流量分析提供了新的解决方案。这对于网络管理员、安全专家和系统设计者来说是一个值得关注的研究方向，因为它有可能推动DPI技术的进一步发展和应用。
that state U has outgoing transitions labeled by the charac-
ters c and d, and that its parent is R, which is the root of a
default transition tree. The content label for transitions en-
tering state V is ab,cd,R. This tells us that state V has outgo-
ing transitions labeled by the characters a and b, and that its
parent (in the default transition tree) has outgoing transi-
tions labeled by the characters c and d, and that its parent’s
parent is R, which is the root of a default transition tree.
Suppose that the current state of the D
2
FA is one of the
predecessors of state V and that the current input character
selects a content label for a transition to state V and that the
next input character is x. While V is the next state, since V
has no labeled transition for x, we would like to avoid visit-
ing state V so that we can skip the associated memory ac-
cess. Similarly, we would like to avoid visiting state U,
since it also has no labeled transition for x. Assume that we
have a hash function h for which h(cd,R)=U and for which
h(ab,U)=V. Given the content label ab,cd,R (which is
stored at the predecessor state), we can determine that nei-
ther our immediate next state (V) nor its parent (U) has an
outgoing transition for x. Hence, we can proceed directly to
R. If on the other hand, the next input character is c or d,
then we can proceed directly to U by computing h(cd,R).
Similarly, if the next input character is a or b, we can pro-
ceed directly to V by computing h(ab,h(cd,R)).
Summarizing, we associate a content label with every
state in a D
2
FA. Each label includes a character set for the
state and each of its ancestors in the default transition tree,
plus a number identifying the state at the root of the tree.
We augment the content label with a bit string that indicates
which of the states on the path from the given state to the
root of its tree are matching states for the automaton. In our
examples, we use underlining of the character set for a
given state to denote that the state is a matching state. So, if
state U in our example matched an input pattern of interest,
we would write the content label for U as cd
,R and the con-
tent label for V as ab,cd
,R. Content labels are stored at
predecessor states, and hashing is used to map the labels to
the next state that we need to visit.
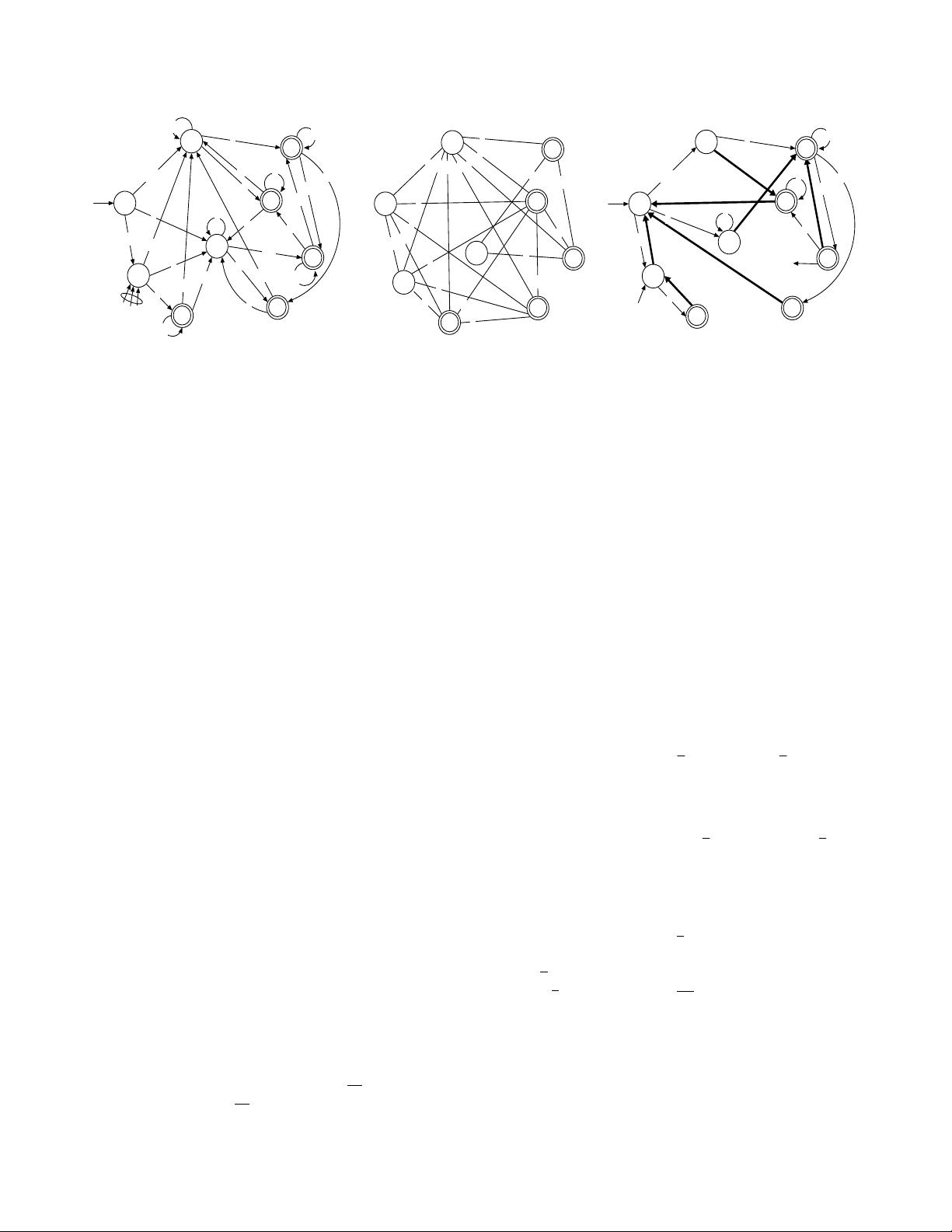
3.2 Complete Example
We now turn to a more complete example. Figure 2a shows
a DFA that matches the patterns a[aA]
+
b
+
, [aA]
+
c
+
, b
+
[aA]
+
,
b
+
[cC] and dd
+
. Part b of the figure shows a corresponding
space reduction graph and part c shows a D
2
FA constructed
using this space reduction graph. The default transitions are
shown as bold edges. Note that states 1 and 8 are roots of
their default transition trees and that the longest sequence of
default transitions that can be followed without consuming
an input character is 2. If we use the D
2
FA to parse an input
string, the number of memory accesses can be as large as
three times the number of characters in the input string.
Consider a parse of the string aAcba. Using the original
DFA, we can write this in the form
956441 →→→→→
abcAa
Here, the underlined state numbers indicate matching states.
Using the D
2
FA, we the parse of the string will be
98156661441 →→→→→
abcAa
Here, we are showing the intermediate states traversed by
the D
2
FA. To specify the CD
2
FA, we first need to write the
content labels for each of the states. These are listed below.
Note that since states 3 and 7 have no labeled outgoing
transitions in the D
2
FA, their content labels include empty
character sets that are indicated by dashes. The dash in the
content label for state 3 is underlined to indicate that state 3
is a matching state.
6. c,1
7. –,1
8. 8
9. cC
,8
1. 1
2. d,1
3. –
, d,1
4. b,c
,1
5.
b
,8
1
4
5
8
9
6
a,A
b
c
b
a,A
b
c
a,A
b
c
b
a,A
a,A
2
b
d
7
c,C
a,A
b
a,A
b
d
1
4
5
8
9
6
2
7
6
5
6
5
7
6
7
7
7
5
8
7
5
c,C
6
a,A
5
7
d
From
states 4-9
3
d
a,A
b
3
8
5
7
6
7
1
4
5
8
9
6
a,A
b
b
c
a,A
b
c
2
b
d
7
c,C
d
From
state 8
3
d
C
to state 1
Figure 2. a) DFA recognizing patterns [aA]
+
b
+
, [aA]
+
c
+
, b
+
[aA]
+
, b
+
[cC], and dd
+
over alphabet {a, b, c, d, A, B, C, D} (transitions
for characters not shown in the figure leads to state 1). b) Corresponding space reduction graph (only edges of weight greater
than 4 are shown). c) A set of default transition trees (tree diameter bounded to 4 edges) and the resulting D
2
FA.
剩余10页未读，继续阅读
点击了解资源详情
点击了解资源详情
点击了解资源详情
2009-12-08 上传
2018-04-29 上传
2021-04-22 上传
2017-10-23 上传
2022-09-23 上传
2018-06-10 上传
daniel3
- 粉丝: 1
- 资源: 4
我的内容管理
展开
最新资源
- WordPress作为新闻管理面板的实现指南
- NPC_Generator：使用Ruby打造的游戏角色生成器
- MATLAB实现变邻域搜索算法源码解析
- 探索C++并行编程：使用INTEL TBB的项目实践
- 玫枫跟打器：网页版五笔打字工具，提升macOS打字效率
- 萨尔塔·阿萨尔·希塔斯：SATINDER项目解析
- 掌握变邻域搜索算法：MATLAB代码实践
- saaraansh: 简化法律文档，打破语言障碍的智能应用
- 探索牛角交友盲盒系统：PHP开源交友平台的新选择
- 探索Nullfactory-SSRSExtensions: 强化SQL Server报告服务
- Lotide：一套JavaScript实用工具库的深度解析
- 利用Aurelia 2脚手架搭建新项目的快速指南
- 变邻域搜索算法Matlab实现教程
- 实战指南：构建高效ES+Redis+MySQL架构解决方案
- GitHub Pages入门模板快速启动指南
- NeonClock遗产版：包名更迭与应用更新
