北京林业大学详解DDA直线生成算法及其在计算机图形中的应用

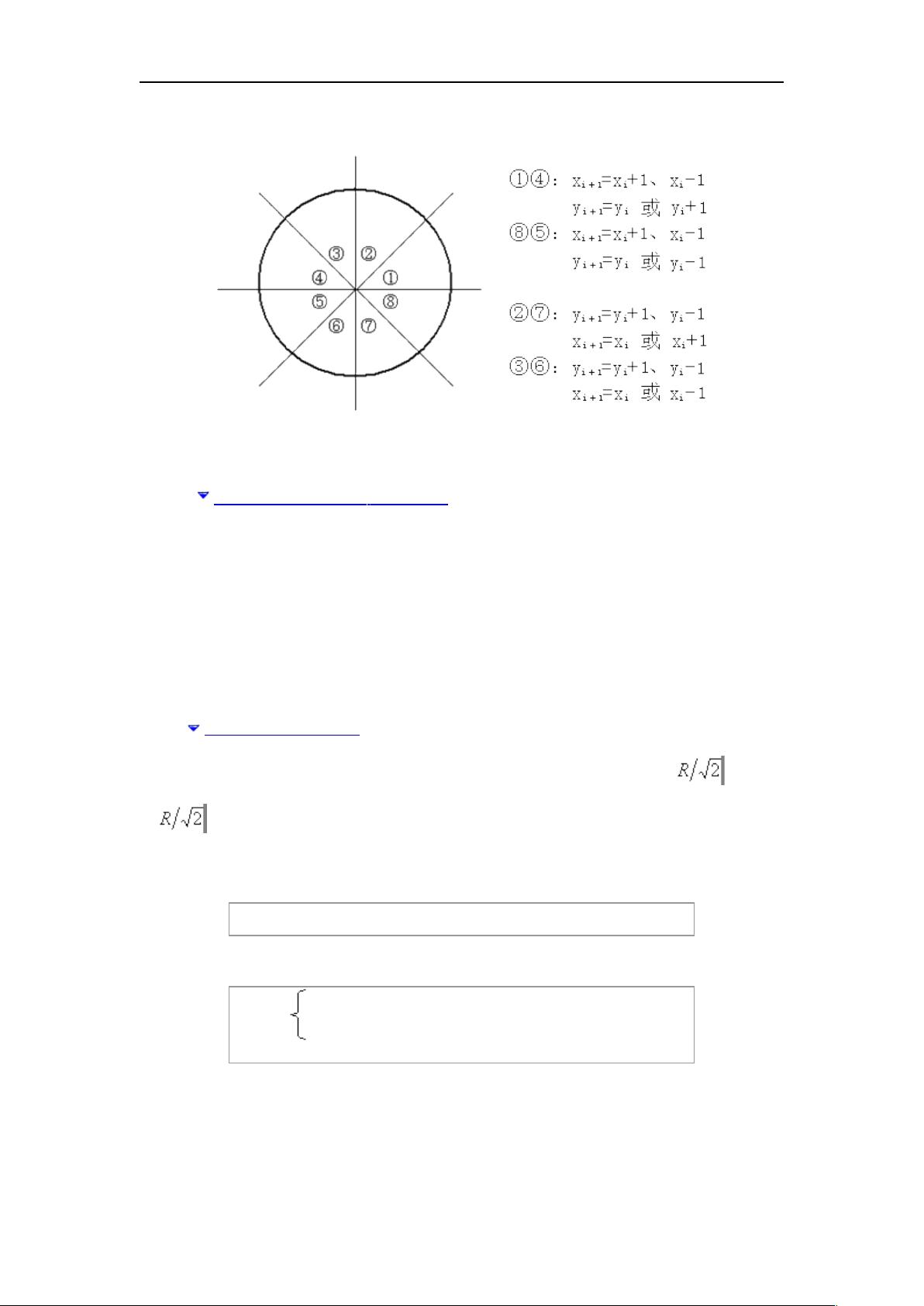
北京林业大学计算机图形学课程中，DDA（Digital Differential Analyzer，数字微分分析器）算法是教学中的一个重要部分，特别是在考试中经常被考察。DDA算法主要用于生成二维平面上的直线，其核心原理是基于直线的微分方程，通过逐像素的方式将直线划分为小段并进行扫描转换。 算法的基本步骤如下： 1. **直线DDA算法描述**： - 给定起点(x1, y1)和终点(x2, y2)，首先计算直线的斜率m = (y2 - y1) / (x2 - x1)。 - 选择较大的增量方向，通常以像素为单位，例如如果x2-x1较大，取dx = 1，dy = m。 - 使用递推公式 xi+1 = xi + △x 和 yi+1 = yi + △y，其中△x 和 △y 按照相应方向计算。 - 将计算出的坐标进行取整后，送入显示器输出，形成连续的像素点，实现直线的扫描转换。 2. **算法思想**： - 选择较大的增量保证了像素分布的均匀性，使得在显示的线段上像素间距一致。 - 考虑生成方向确保Δx和Δy的正负，避免重复或者跳过像素。 3. **算法实现**： - 输入参数包括直线两端点坐标、颜色以及初始位置。 - 计算增量变量dx和dy，确定最大变化量steps。 - 根据最大变化量确定每个像素的增量xin和yin。 - 通过循环结构，每次将当前像素点颜色设置为给定颜色，然后根据增量更新坐标，直至遍历完整个步长。 DDA算法因其简单易懂和适合硬件实现，在教学中常用于基础图形学教学，让学生了解基本的图像处理原理。然而，对于精度要求较高的应用，如计算机图形渲染或矢量图形处理，它可能不如更复杂的算法如Bresenham算法或Floyd-Steinberg算法。掌握这个算法对于理解图形学的基础和准备考试来说都是非常关键的。