理解SVM：从基础到核函数的统计学习方法

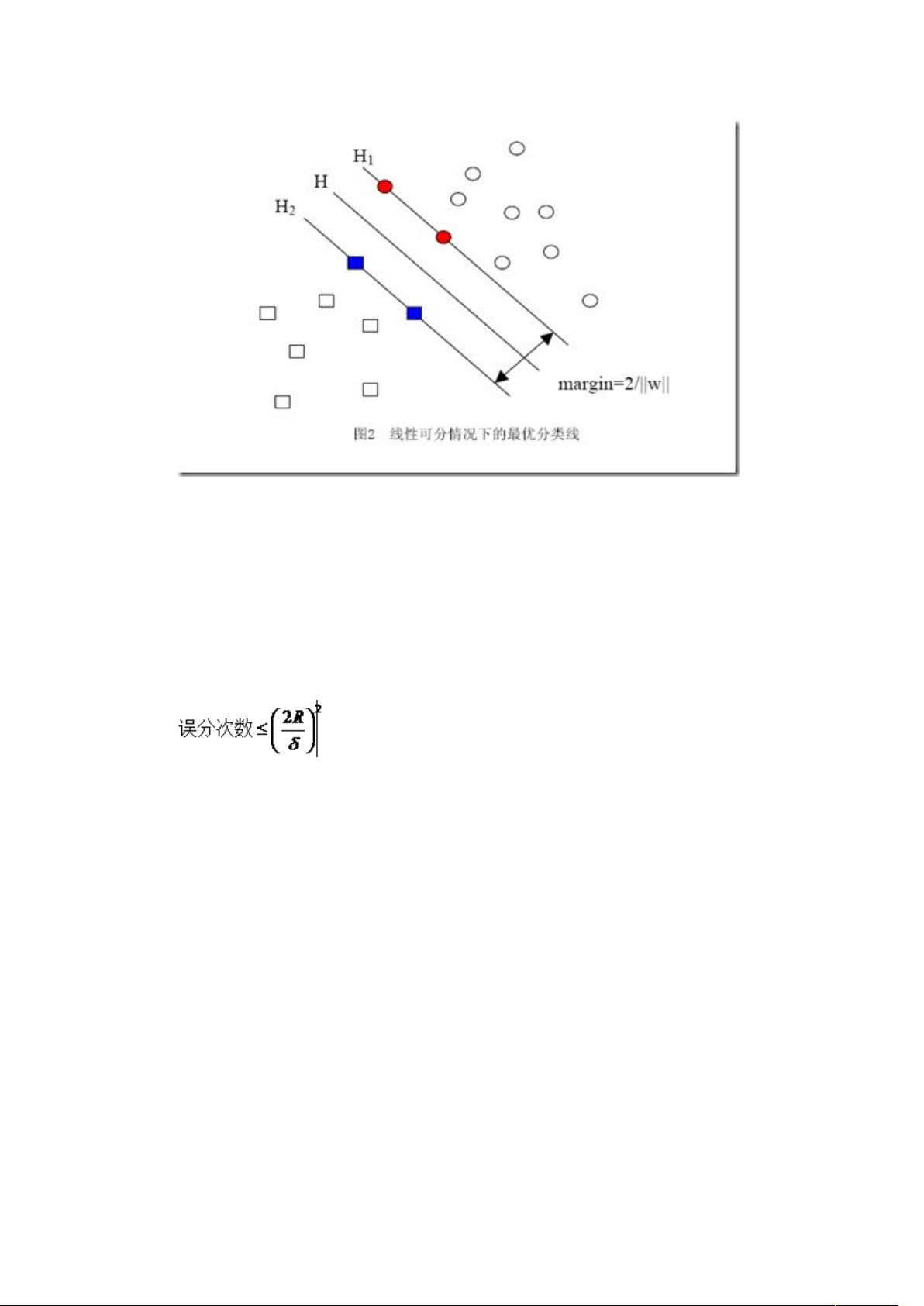
"svm轻松入门(好文章)" 支持向量机（Support Vector Machine，简称SVM）是一种基于统计学习理论的二分类模型，由Cortes和Vapnik于1995年提出。SVM的核心理念是寻找一个最优的超平面，这个超平面能够将不同类别的数据点最大程度地分开，同时最小化误分类的风险。SVM在处理小样本、非线性和高维数据时表现出了强大的能力，因此在模式识别、文本分类、生物信息学等领域得到了广泛应用。 SVM的理论基础主要包括统计学习理论中的VC维理论和结构风险最小化原理。VC维（Vapnik-Chervonenkis Dimension）是一个衡量模型复杂度的概念，它决定了模型能够正确分类数据集的最大样本容量。低VC维意味着模型更简单，可能过拟合；高VC维则可能导致模型过于复杂，容易欠拟合。SVM通过选取合适的超平面，尽可能降低VC维，从而提高泛化能力。 结构风险最小化是SVM优化目标的关键。它强调在学习过程中不仅要考虑模型在训练集上的表现（即经验风险），还要考虑模型对未知数据的预测能力（即期望风险）。通过在两者之间找到平衡，SVM试图找到一个具有最佳泛化能力的模型。在实际操作中，SVM通过引入软间隔和惩罚项，允许一部分数据点可以被误分类，但同时会相应增加模型的复杂度，从而实现结构风险的最小化。 SVM的一个独特之处在于其核函数机制。当原始数据不是线性可分时，SVM可以通过非线性核函数将数据映射到高维空间，在这个新的空间中寻找线性超平面进行分类。常见的核函数有线性核、多项式核、高斯核（RBF）等，不同的核函数对应不同的非线性映射，使得SVM能够处理各种复杂的非线性问题。 SVM的训练过程包括求解一个凸优化问题，这保证了SVM存在全局最优解，避免了局部最优的问题。在训练完成后，支持向量（Support Vectors）是距离超平面最近的数据点，它们对决策边界的影响最大，因此得名。 在实际应用中，SVM的参数调整至关重要，如惩罚系数C和核函数参数γ等。这些参数的选择会直接影响模型的性能和复杂度。此外，面对大规模数据集时，SVM的训练时间可能会很长，这时可以采用如SVM的在线学习算法或者近似算法来提高效率。 SVM是一种强大且灵活的机器学习算法，其理论严谨，能够处理高维和非线性问题，适用于多种应用场景。然而，理解和掌握SVM需要一定的数学基础，特别是对优化理论和统计学习理论的理解。通过深入学习和实践，我们可以更好地利用SVM解决实际问题。