"线性代数课题报告总结:课本内容定义与知识总结"
需积分: 28 106 浏览量
更新于2024-02-02
收藏 1.88MB DOCX 举报
线性代数是数学的一个重要分支,研究向量空间、线性变换和线性方程组等基本概念及其相互关系的数学理论。本线性代数课题报告分为两部分,一部分是关于课本内容的定义,另一部分是对课本知识的总结。
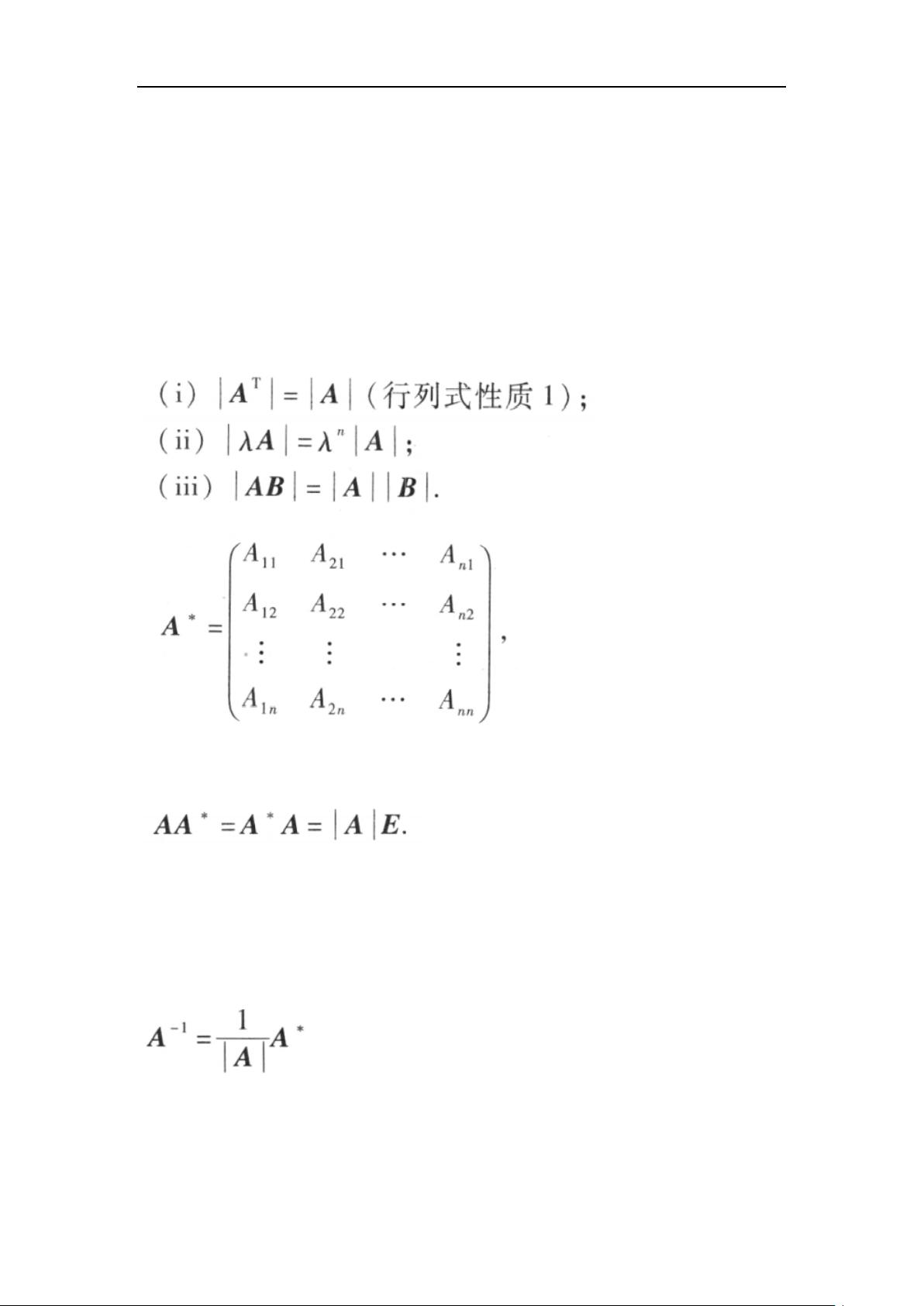
在课本内容定义的部分中,首先介绍了行列式的概念和性质。行列式是一个矩阵所对应的一个数值,它反映了矩阵的重要特征,比如矩阵的奇偶性、可逆性等。然后对线性代数的基本概念进行了介绍,包括向量、向量的线性组合、向量空间等。向量是线性代数中的基本概念,它是具有大小和方向的量,可以进行加法和数乘运算。向量的线性组合是指通过对向量进行加法和数乘运算得到的新向量,这是线性代数中非常重要的一个概念。向量空间则是由一组向量经过线性组合得到的所有可能的向量的集合,具有一定的性质和结构。另外,课本内容定义部分还介绍了线性变换和特征值、特征向量的概念,这些是线性代数的核心内容。
在课本知识总结部分,对课本中的重要知识点进行了回顾和总结。首先总结了行列式的计算方法和性质,包括如何计算二阶和三阶行列式,以及行列式的性质和应用。接着总结了向量及其线性组合的相关知识,包括向量的加法、数乘、线性相关性、线性无关性等。然后总结了对矩阵的相关知识,包括矩阵的加法、数乘、矩阵乘法、逆矩阵、转置矩阵等。对于线性方程组的解的讨论和求解方法也进行了总结,包括高斯消元法、矩阵求逆法、克拉默法则等。最后总结了线性变换、特征值和特征向量的相关知识,包括线性变换的定义和性质、特征值和特征向量的计算方法和应用等。
总的来说,线性代数是一个复杂而又有趣的数学分支,它不仅在数学理论上有着重要的地位,而且在现代科学和工程技术中也有着广泛的应用。通过本次课题报告的学习,对线性代数的基本概念和知识有了更深入的了解和掌握,对于将来在相关领域的学习和工作都具有一定的帮助和指导作用。同时也希望未来可以进一步深入研究线性代数,探索其中的新知识和新应用,为科学和技术的发展做出更大的贡献。
2011-06-22 上传
2021-09-25 上传
2023-09-02 上传
2012-11-21 上传
2024-03-18 上传
2021-09-22 上传
俊颖463
- 粉丝: 16
- 资源: 14
最新资源
- 基于Python和Opencv的车牌识别系统实现
- 我的代码小部件库:统计、MySQL操作与树结构功能
- React初学者入门指南:快速构建并部署你的第一个应用
- Oddish:夜潜CSGO皮肤,智能爬虫技术解析
- 利用REST HaProxy实现haproxy.cfg配置的HTTP接口化
- LeetCode用例构造实践:CMake和GoogleTest的应用
- 快速搭建vulhub靶场:简化docker-compose与vulhub-master下载
- 天秤座术语表:glossariolibras项目安装与使用指南
- 从Vercel到Firebase的全栈Amazon克隆项目指南
- ANU PK大楼Studio 1的3D声效和Ambisonic技术体验
- C#实现的鼠标事件功能演示
- 掌握DP-10:LeetCode超级掉蛋与爆破气球
- C与SDL开发的游戏如何编译至WebAssembly平台
- CastorDOC开源应用程序:文档管理功能与Alfresco集成
- LeetCode用例构造与计算机科学基础:数据结构与设计模式
- 通过travis-nightly-builder实现自动化API与Rake任务构建