JS浮点数精度问题解析与解决方案

"JS浮点数运算结果不精确的Bug解决" JS中的浮点数运算结果不精确，这是由于JavaScript内部数字类型Number是基于IEEE-754标准的双精度浮点数（double precision）来存储和计算的。在二进制系统中，某些十进制小数无法精确表示，导致在进行加、减、乘、除等运算时出现精度误差，这对于涉及财务或精确计算的场景尤为关键。 常见例子展示了浮点数运算的不精确性，例如： 1. 加法：0.1 + 0.2 不等于预期的0.3，而是0.30000000000000004；0.1 + 0.7 不等于0.8，而是0.7999999999999999；0.2 + 0.4 不等于0.6，而是0.6000000000000001。 2. 减法：0.3 - 0.2 不等于0.1，而是0.09999999999999998；1.5 - 1.2 不等于0.3，而是0.30000000000000004。 3. 乘法：0.8 * 3 不等于2.4，而是2.4000000000000004；19.9 * 100 不等于1990，而是1989.9999999999998。 4. 除法：0.3 / 0.1 不等于3，而是2.9999999999999996；0.69 / 10 不等于0.069，而是0.06899999999999999。 5. 比较：如0.1 + 0.2 不等于 0.3，导致0.1 + 0.2 === 0.3 为假，同样的，(0.3 - 0.2) !== (0.2 - 0.1) 也为假。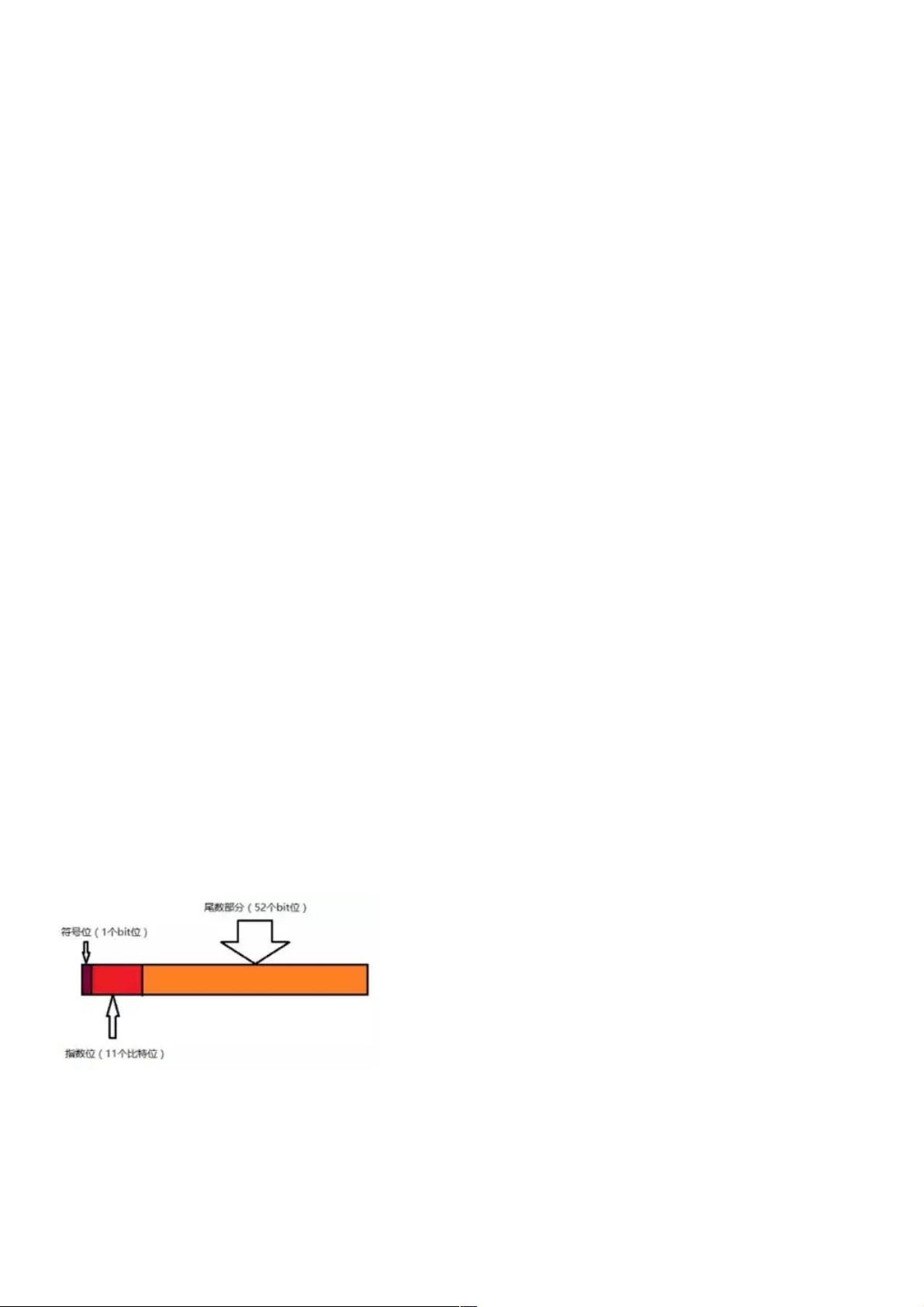 这种不精确性源于IEEE 754标准的浮点数表示方法。在64位的双精度浮点数中，1位用于表示符号（0为正，1为负），11位用于表示指数，剩下的52位用于表示尾数（mantissa）。由于指数和尾数的限制，有些十进制小数无法精确地转换为二进制，因此在进行运算时会产生微小的误差。 解决JS浮点数运算不精确的方案有多种： 1. 使用toFixed()方法将结果四舍五入到指定的小数位数，但这种方法并不适用于比较操作。 2. 使用BN.js或decimal.js等库，它们提供了高精度的数学运算，能够处理浮点数的精度问题。 3. 对于货币计算，可以使用整数表示金额，比如用分代替元，这样可以避免浮点数运算的不精确性。 4. 对于比较操作，可以采用绝对误差的比较，即判断两个数之差的绝对值是否小于一个极小的阈值。 理解这些原理和解决方案后，开发者在遇到JS浮点数精度问题时就能更加得心应手，避免因浮点数运算的不精确性导致的潜在错误。在实际开发中，选择合适的策略处理浮点数运算，对于确保财务计算的准确性至关重要。