希尔伯特线性方程组数值求解：病态性、G-S迭代与CG方法

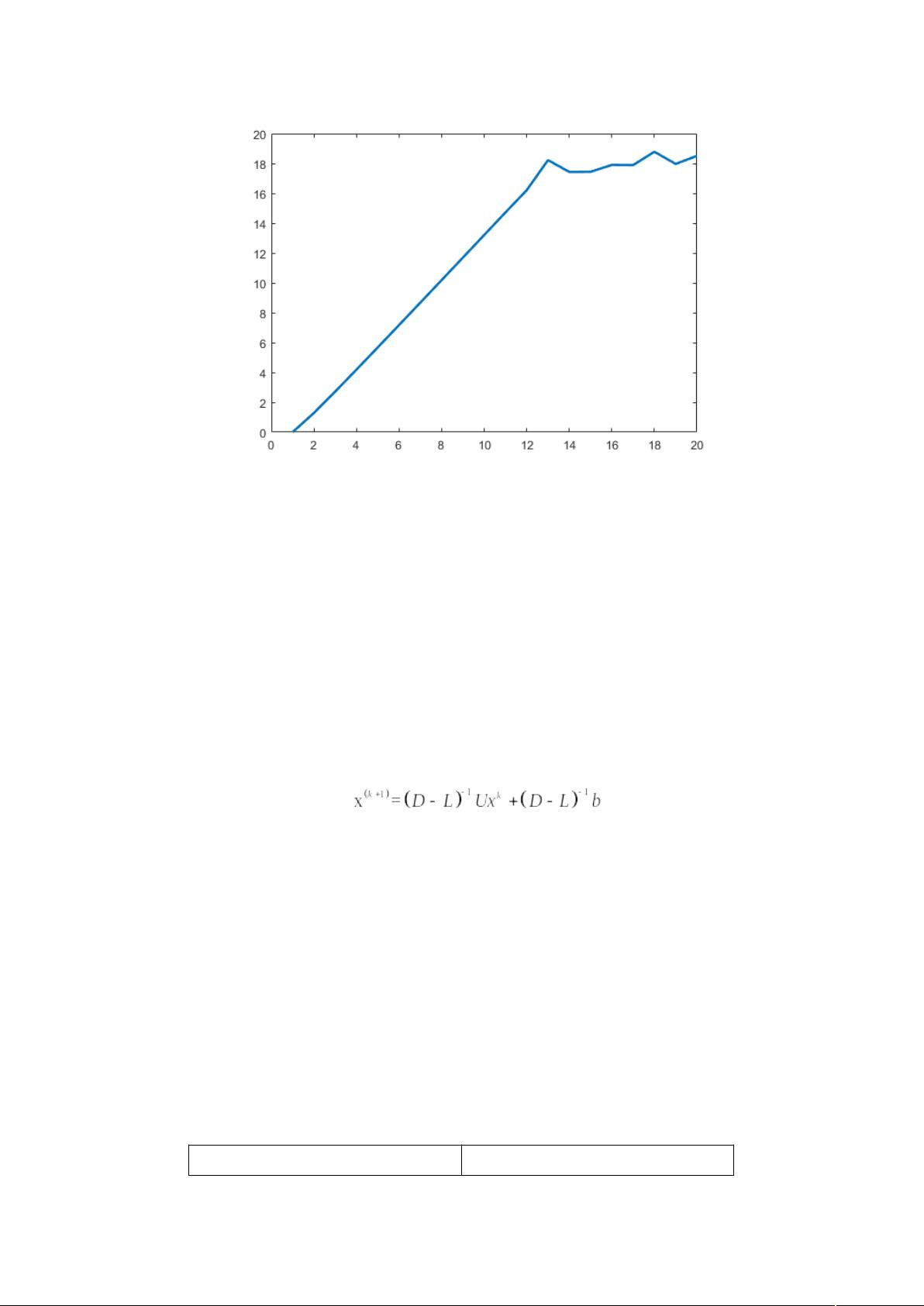
希尔伯特线性方程组数值求解是一篇关于在数值分析领域中解决特定类型的线性方程组的研究。希尔伯特方程组源于寻找一个n次多项式，使其对某个函数的最佳平方逼近，并通过极值条件得到一个线性方程组。这个方程组的核心是希尔伯特矩阵，它是一个对称且正定的矩阵，但在实际应用中，特别是当矩阵阶数增大时，会出现显著的病态性，即矩阵条件数快速增大，导致数值稳定性问题。 在处理高阶希尔伯特矩阵时，标准的MATLAB计算方法在矩阵阶数超过一定范围后变得困难，因为条件数的增长导致计算精度丧失。为了解决这个问题，文章介绍了几种数值求解方法： 1. 高斯-赛德尔迭代法：这是一种迭代求解线性方程组的方法。作者尝试了初始设置的最大迭代次数为500次，但未能达到预期精度，随后提高至1000次才获得满足0.0001误差限的解，迭代859次后得到的解向量在数值上稳定。 2. 最速下降法：这种方法利用函数的负梯度方向进行迭代。尽管设置了最大迭代次数为1000次，最速下降法仅需423次迭代就达到误差为9.917e-05，但同样受限于计算机的舍入误差。 3. 共轭梯度法：这是一种高效的迭代方法，它选择系数矩阵的共轭向量作为迭代方向。理论上来讲，共轭梯度法能在n步内找到精确解，但实践中需要设定残差向量范数作为停止迭代的标准，以应对计算机误差。这种方法与前两者相协调，提供了更合理的求解策略。 本文主要探讨了希尔伯特线性方程组的数学背景，矩阵的特性，以及在面对病态性时如何通过迭代方法，如高斯-赛德尔法、最速下降法和共轭梯度法来求解，并对比了它们在实际计算中的性能和适用性。数值分析中的矩阵病态性和求解算法的有效性是本研究的关键知识点。