CSci 235 Software Design and Analysis II
Introduction to Recursion
Prof. Stewart Weiss
pairs must be the number of pairs alive in month
n − 1
, plus the number of new ospring born at the start
of month
n
. All pairs alive in month
n − 2
contribute their pair in month
n
, so there are
f(n − 1) + f(n − 2)
rabbit pairs alive in month
n
. The recursive denition of this sequence is thus
f (n) =
(
1 if n ≤ 2
f(n − 1) + f (n − 2) if n > 2
This will generate the sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and so on. A recursive algorithm to
compute the nth Fibonacci number, for
n > 0
, is given below, written as a C/C++ function.
int fibonacci (int n)
{
if ( n <= 2 )
return 1;
else
return fibonacci(n-1) + fibonacci(n-2);
}
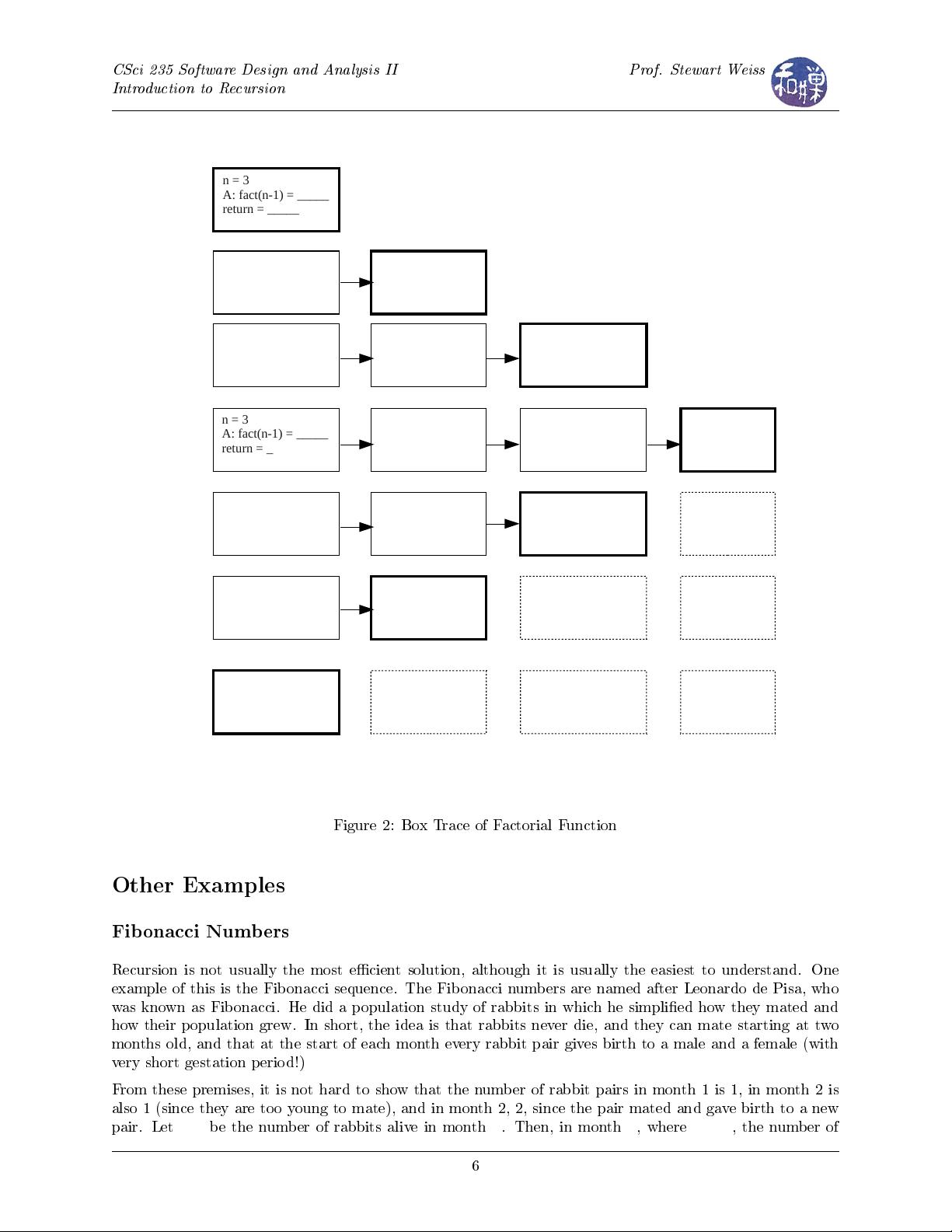
Although this looks simple, it is very inecient. If you write out a box trace of this function you will see
that it leads to roughly
2
n
function calls to nd the
n
th
Fibonacci number. This is because it computes
many values needlessly. There are far better ways to compute these numbers.
Choosing k Out of n Objects
A well-known and common combinatorial (counting) problem is how many distinct ways there are to pick
k
objects from a collection of
n
distinct objects. For example, if I want to pick 10 students in the class of 30,
how many dierent sets of 10 students can I pick? I do not care about the order of their names, just who is
in the set. Let
c(n, k)
represent the number of distinct sets of
k
objects out of a collection of
n
objects.
The solution can be dicult to nd with a straight-forward attack, but a recursive solution is quite simple.
Let me rephrase the problem using the students in the class. Suppose I single out one student, say student
X. Then there are two possibilities: either X is in the group I choose or X is not in the group.
How many solutions are there with X in the group? Since X is in the group, I need to pick
k − 1
other
students from the remaining
n − 1
students in the class. Therefore, there are
c(n − 1, k − 1)
sets that contain
student X.
What about those that do not contain X? I need to pick
k
students out of the remaining
n − 1
students in
the class, so there are
c(n − 1, k)
sets.
It follows that
c(n, k) = c(n − 1, k − 1) + c(n − 1, k)
when
n
is large enough. Of course there are no ways to form groups of size
k
if
k > n
, so
c(n, k) = 0
if
k > n
. If
k = n
, then there is only one possible group, namely the whole class, so
c(n, k) = 1
if
k = n
. And
if
k = 0
, then there is just a single group consisting of no students, so
c(n, k) = 1
when
k = 0
. In all other
cases, the recursive denition applies. Therefore the recursive denition with its base cases, is
c(n, k) =
1 k = 0
1 k = n
0 k > n
c(n − 1, k − 1) + c(n − 1, k) 0 < k < n
Once again it is easy to write a C/C++ function that computes this recursively by applying the denition:
7