Cannon算法实现矩阵相乘并行计算
版权申诉
59 浏览量
更新于2024-08-12
收藏 835KB DOCX 举报
"Cannon方法是一种用于并行计算矩阵相乘的高效算法,尤其适用于进程数为完全平方数的情况。该方法通过分布式存储矩阵并利用多个进程同步操作来提高计算速度。"
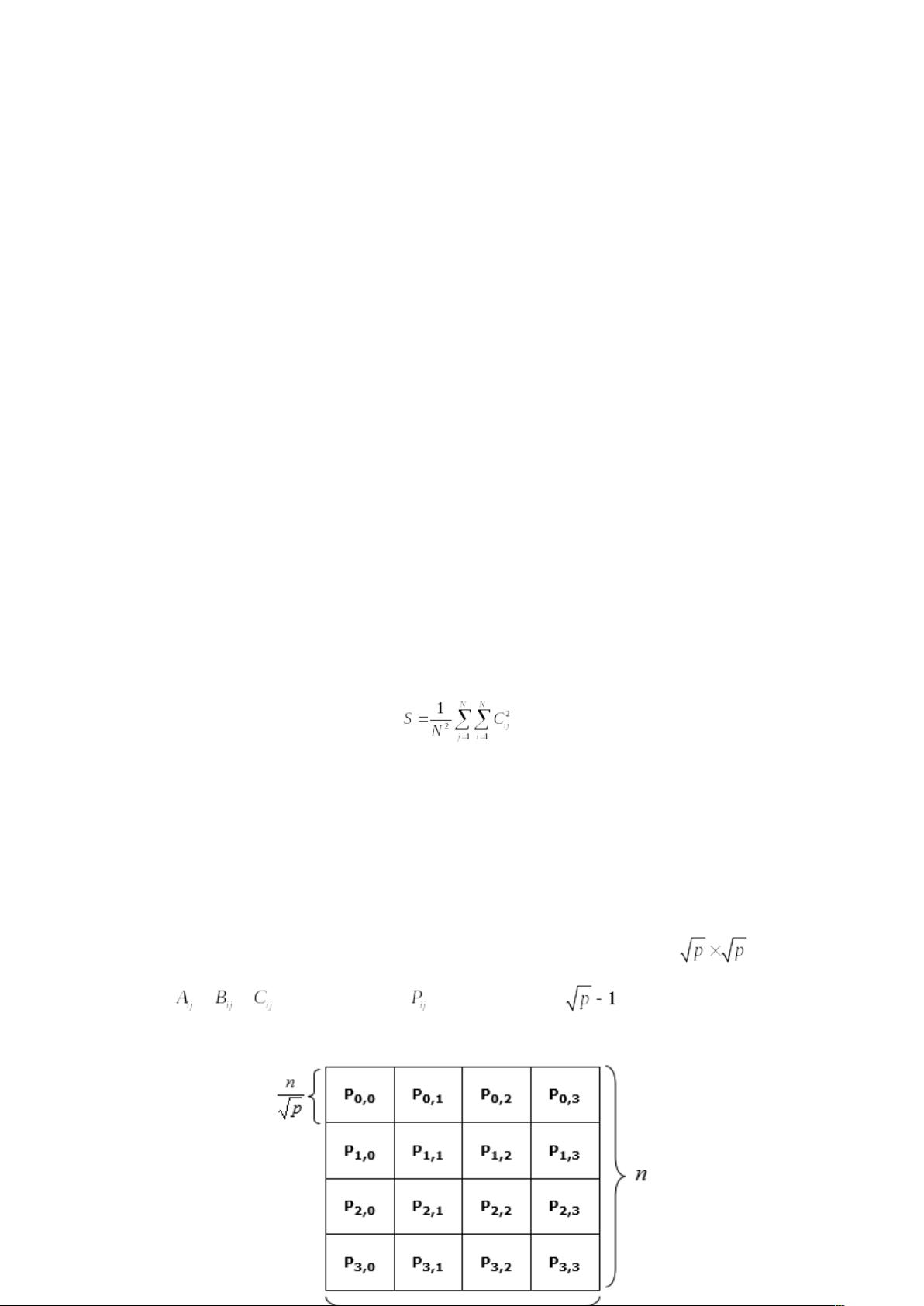
Cannon方法的核心思想是将大矩阵A、B和结果矩阵C分割成小的方块,每个方块分配给一个单独的进程处理。当进程数P是完全平方数时,这些进程可以排列成一个P×P的网格,其中矩阵块按照网格的位置存储。Cannon算法包括四个主要步骤,通过循环移动和并行乘法操作来实现矩阵相乘。
1. **初始化**: 所有进程首先确定其在网格中的位置(行号i和列号j),这可以通过进程ID除以和取模sqrt(P)得到。
2. **块移动**: 按照算法,所有块Aij向左循环移动i步,所有块Bij向上循环移动j步。这个过程确保了正确对齐的矩阵块可以进行乘法操作。
3. **乘加运算**: 当块移动完成后,同一网格位置上的Aij和Bij进行乘法运算,然后将结果累加到对应位置的Cij上。这个步骤是并行进行的,所有处理器Pij执行乘加运算。
4. **块循环移动**: 完成一次乘法后,所有Aij向左移动一步,所有Bij向上移动一步,然后重复步骤2和3。这个过程持续L次,L为子块的维度(N/m,N是矩阵的大小,m是sqrt(p))。
`LeftMoveOneStep()`函数负责将当前进程存储的A子块发送给左侧进程,同时接收右侧进程的A子块,这样就能实现块的循环移动。同样,`UpMoveOneStep()`函数处理块的上移操作。
为了验证程序的正确性,需要计算C矩阵并与串行程序的结果进行比较,即计算S值。此外,还需要在不同N值(100, 200, 500)和不同进程数(1, 2, 4, 10)下运行程序,并使用`MPI_Wtime()`函数记录运行时间,从而评估程序的加速比。加速比是并行程序运行时间与串行程序运行时间的比率,反映了并行计算的有效性。
在实际应用中,Cannon方法可以显著提高大规模矩阵相乘的效率,特别是在拥有大量并行处理资源的环境中。然而,由于它依赖于进程数为完全平方数,因此可能不适用于所有情况。对于非完全平方数的进程数,可以采用其他并行矩阵乘法算法,如Strassen、Fox、Systolic或DNS等。
点击了解资源详情
点击了解资源详情
点击了解资源详情
2021-11-23 上传
2011-11-21 上传
2022-10-17 上传
2023-10-19 上传
2012-01-13 上传
2011-06-30 上传
joeduolala
- 粉丝: 0
- 资源: 954
最新资源
- EagleEyeVision.github.io
- winter-semester-study-report:撰写学习报告
- kafka-node-dotnetcore:示例,使用Kafka,服务提供商实施节点,节点服务提供商实施Dotnet核心
- CCNA_Networking_Fundamentals_Course:完整的网络基础课程-CCNA,讲师
- primus-analytics:使用事件跟踪将 Google Analytics 深度集成到 Primus
- metPath:代谢组学数据的途径富集
- NOVA - нова начална страница-crx插件
- camera-app-test:测试手机相机应用程序
- aabbtree-2.6.2-py2.py3-none-any.whl.zip
- ObsWebApplication
- Pewlett-Hackard分析
- 86-DOS 1.0 [SCP OEM] [SCP Cromemco 4FDC] (4-30-1981) (8 inch SSSD).rar
- ACCESS网上远程教育网ASP毕业设计(开题报告+源代码+论文+答辩).zip
- Extibax-Portfolio-CSS3-JS-JQuery:这是Extibax Portfolio V2,是一个很棒的Portfolio,我完成了重要的开发,请转到此页面的末尾以获取更多信息
- backend-jobsite
- Foldable-Robots-Team-2