图解TCP-IP协议：弱信号下的GPS跟踪技术分析
需积分: 9 105 浏览量
更新于2024-09-09
1
收藏 1.87MB PDF 举报
"图解TCP-IP协议的学习资料"
在深入探讨TCP/IP协议之前，我们先理解一下TCP（传输控制协议）和IP（网际协议）的基本概念。TCP是一种面向连接的、可靠的传输协议，它确保数据包按照正确的顺序无差错地发送到目标地址。而IP则负责在网络中将数据包路由到正确的目的地。两者结合，构成了互联网通信的基础。
日本村上所著的《图解TCP/IP协议》是一本极好的学习资源，它通过图形化的方式帮助读者理解和掌握TCP/IP协议栈的各个层次，包括应用层、传输层、网络层和数据链路层。这本书不仅涵盖了基本概念，还深入讨论了协议的工作原理和实际应用。
在部分内容中提到的"Weak GPS signal tracking using FFT discriminator in open loop receiver"是一个与GPS接收机相关的技术，虽然与TCP/IP协议不是直接相关，但可以作为一个拓展知识。GPS接收机在弱信号环境下，需要有高效的跟踪算法来保持对卫星信号的锁定。文中介绍的开放式循环跟踪架构，使用快速傅里叶变换（FFT）鉴频器来估计单音复信号的多普勒频率残余，从而在信号强度低且环境挑战性大的情况下跟踪GPS信号。
FFT作为一种强大的数字信号处理工具，被用于频率分析。在这里，它被用来作为频率歧视器，估计单音信号的多普勒频率，即GPS信号由于接收机和卫星之间的相对运动产生的频率偏移。另外，通过复数平方的方法，可以消除导航数据位极性的影响，提高跟踪性能。
论文评估了基于FFT的歧视器在三个标准下的性能：可跟踪的信号强度和动态范围，以及估计的多普勒频率的准确性。同时，分析了这些歧视器的理论和模拟峰值检测概率。实验结果证明，FFT歧视器在弱GPS信号跟踪中表现出了良好的性能。
无论是TCP/IP协议的理解还是GPS接收机的信号处理技术，都需要扎实的数学基础和深入的专业知识。《图解TCP/IP协议》提供了一个全面的学习平台，而文中提到的GPS跟踪技术则展示了信号处理在现实世界问题中的应用。这两个主题都对于IT行业的专业人士来说是非常有价值的知识点，能够增强对网络通信和无线定位系统原理的理解。
I
p
ðt
1
Þ¼adðt
1
Þsin cðpdfTÞcos 2pdft
1
þ
T
2
þ du
0
Q
p
ðt
1
Þ¼adðt
1
Þsin cðpdfTÞsin 2pdft
1
þ
T
2
þ du
0
ð4Þ
where t
1
is the start of the integration time and T is the total
integration time.
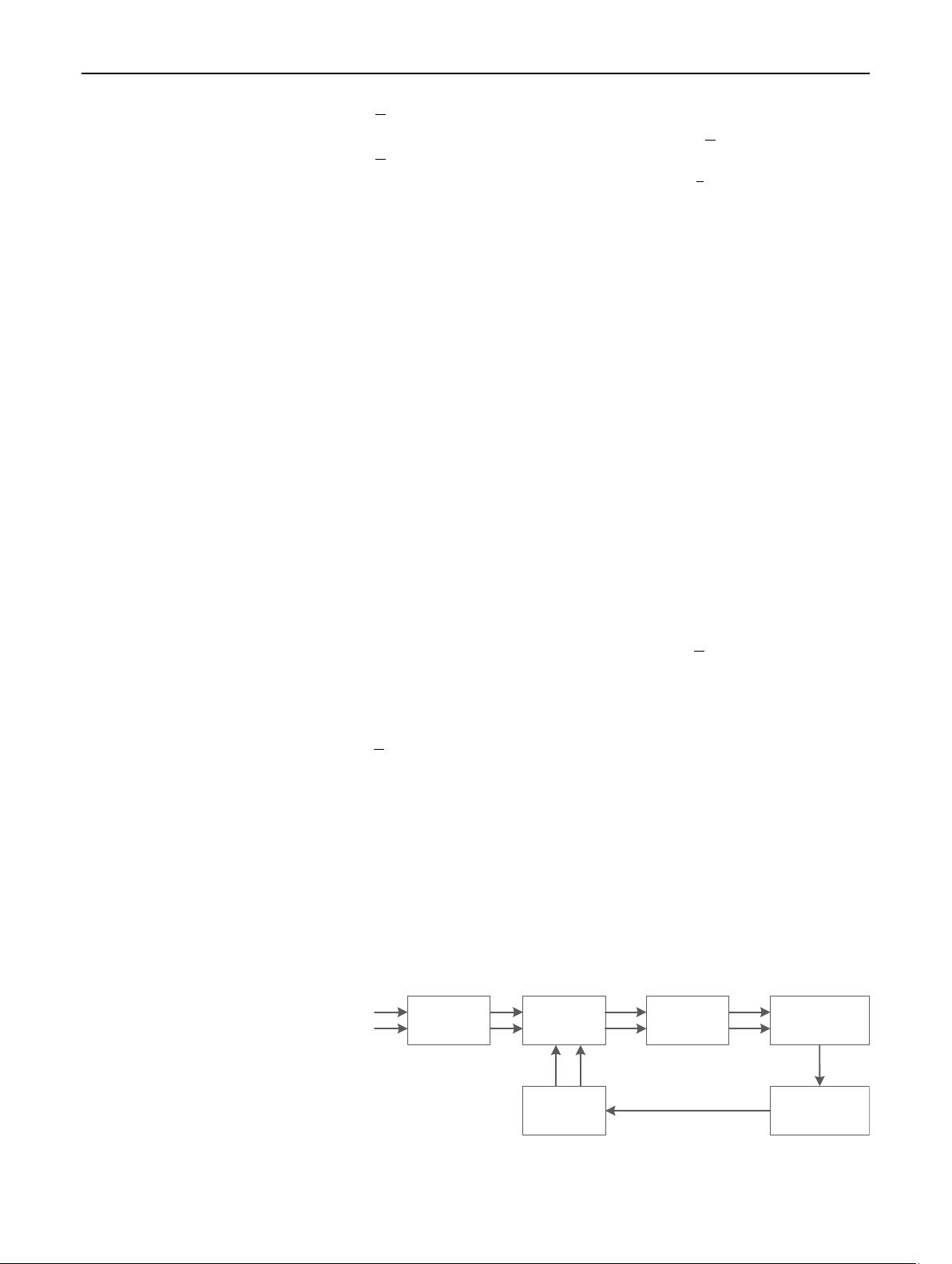
Figure 1 depicts the scheme of a general FLL. The
code and carrier correlators wipe off the PRN code and
the Doppler frequency to get i
p
ðtÞ and q
p
ðtÞ. The inte-
gration and dump module integrates the input signals,
i
p
ðtÞ and q
p
ðtÞ, to get the coherent integration results,
I
p
ðtÞ and Q
p
ðtÞ, respectively. The frequency discriminator
estimates the Doppler frequency residual, d
^
f , from a
series of I
p
ðtÞ and Q
p
ðtÞ. A low-pass loop filter is fol-
lowed to eliminate the high frequency noise in the
estimation. The filtered estimation is then used to control
the NCO, which generates the orthogonal local carrier
signals, i
LO
ðtÞ and q
LO
ðtÞ. This design has a limitation
when using a phase-differential frequency discriminator.
The limitation is that non-coherent integration cannot be
applied because it does not reserve phase information.
Hence, it is not possible to increase the sensitivity
through non-coherent integration.
FFT-based frequency discriminator
The complex form of (4) is:
r
p
ðtÞ¼I
p
ðtÞþjQ
p
ðtÞ
¼ adðtÞsin cðpdfTÞexp j 2pdftþ
T
2
þ du
0
ð5Þ
where adðtÞsincðpdfTÞ is the amplitude of the complex
r
p
ðtÞ which will attenuate with the increase in dfT.Ina
stable tracking state, the frequency residual dfT is rela-
tively small, so the amplitude is approximately adðtÞ.
Hence, r
p
ðtÞ can be expressed as:
r
p
ðtÞ¼I
p
ðtÞþjQ
p
ðtÞ
¼ adðtÞexp j 2pdftþ
T
2
þ du
0
ð6Þ
The phase of expðjð2pdf ðt þ
T
2
Þþdu
0
ÞÞ will rotate with
t, where df determines the rotation speed. The navigation
data bit dðtÞ can be {1, -1} arbitrarily. This will cause a
180° phase reversal in r
p
ðtÞ if the integration is done over
data bits transitions. An assisted GNSS (AGNSS) receiver
can overcome this problem by using aiding information to
predict the data bit values provided it has accurate timing
to within 0.5 ms, eliminate their effect, and overcome the
data bit length limitation (Djuknic and Richton 2001). The
integration time limitation in the GPS L1 C/A signal is
20 ms if the locations of the data bits transitions are
known. However, it is difficult to determine the data bit
transitions in a stand-alone GNSS receiver. Therefore, a
complex squaring operation can be applied to circumvent
the effects of data bits, without the need for determining
the data bits transitions or values. In this operation, the
noise is squared, and so it is not averaged out by summa-
tion. This nonlinear process induces the so-called squaring
loss (van Diggelen 2001). The complex squaring result of
(6) is as follows:
S
p
ðtÞ¼ðI
p
ðtÞþjQ
p
ðtÞÞ
2
¼ I
2
p
ðtÞQ
2
p
ðtÞþj2I
p
ðtÞQ
p
ðtÞ
¼ a
2
exp j22pdftþ
T
2
þ d/
0
ð7Þ
The effect of navigation data bits on S
p
ðtÞ does not exist,
and the frequency and phase of S
p
ðtÞ are doubled. To track
the frequency, the frequency discriminator should estimate
the Doppler frequency residual, d
^
f , from the series S
p
ðtÞ
and then use it to update the NCO.
The proposed frequency discriminator uses the FFT
method to estimate the frequency. Equation (7) shows that
S
p
ðtÞ is a single tone complex signal, where the residual
frequency is its frequency parameter. The frequency of a
single tone complex signal is estimated using FFT. The
adopted FFT approach can be described by:
Carrier
Correlators
Frequency
Discriminator
Code
Correlators
Loop
Filter
NCO
,
()
IF I
s
t
,
()
IF Q
st
()
LO
it
()
LO
qt
Integration
Dump
()
p
it
()
p
qt
()
P
It
()
P
Qt
ˆ
f
δ
Fig. 1 Scheme of general FLL
GPS Solut (2016) 20:225–237 227
123
剩余12页未读，继续阅读
237 浏览量
6665 浏览量
172 浏览量
2010-06-29 上传
123 浏览量
222 浏览量
2010-10-02 上传
211 浏览量
weixin_38906539
- 粉丝: 0
- 资源: 4
我的内容管理
展开
