数据结构深入解析:树与二叉树的概念与应用
需积分: 3 80 浏览量
更新于2024-08-01
收藏 1.12MB PPT 举报
"这是一份关于数据结构中树的课件,适合初学者学习,涵盖了树和二叉树的基本概念、运算、性质、存储结构、遍历、线索化以及树与二叉树的转换,还介绍了Huffman编码的应用。"
在数据结构中,树是一种非常重要的非线性数据结构,它能有效地描述数据的层次关系,因此在系统软件和应用软件设计中广泛使用。树是一种动态结构,允许数据结构进行随机再组织。
树的定义包括以下几点:
1. 树是由n个结点组成的有限集,n可以为0,此时称为空树,记作Φ。
2. 当n大于0时,树有一个称为根的结点,并且其余结点可以分为m个互不相交的子集,每个子集都是根的子树,且每个子树自身也满足树的定义,这是一个递归的概念。
用数学符号表示,树T可以定义为一个二元组T=(D,R),其中D是元素集,R是关系集。如果D为空,则树为空;否则,D包含一个根元素,其余元素是各个子树的元素集,且这些集合互不相交。
例如,IBM PC DOS中的文件结构可以看作一棵树,根结点是MFD,下面有多个子目录和文件,形成了层次结构。同样的,编译系统中,表达式如a+b*(c-b)-e/f可以转换为一棵树来表示,方便处理运算。
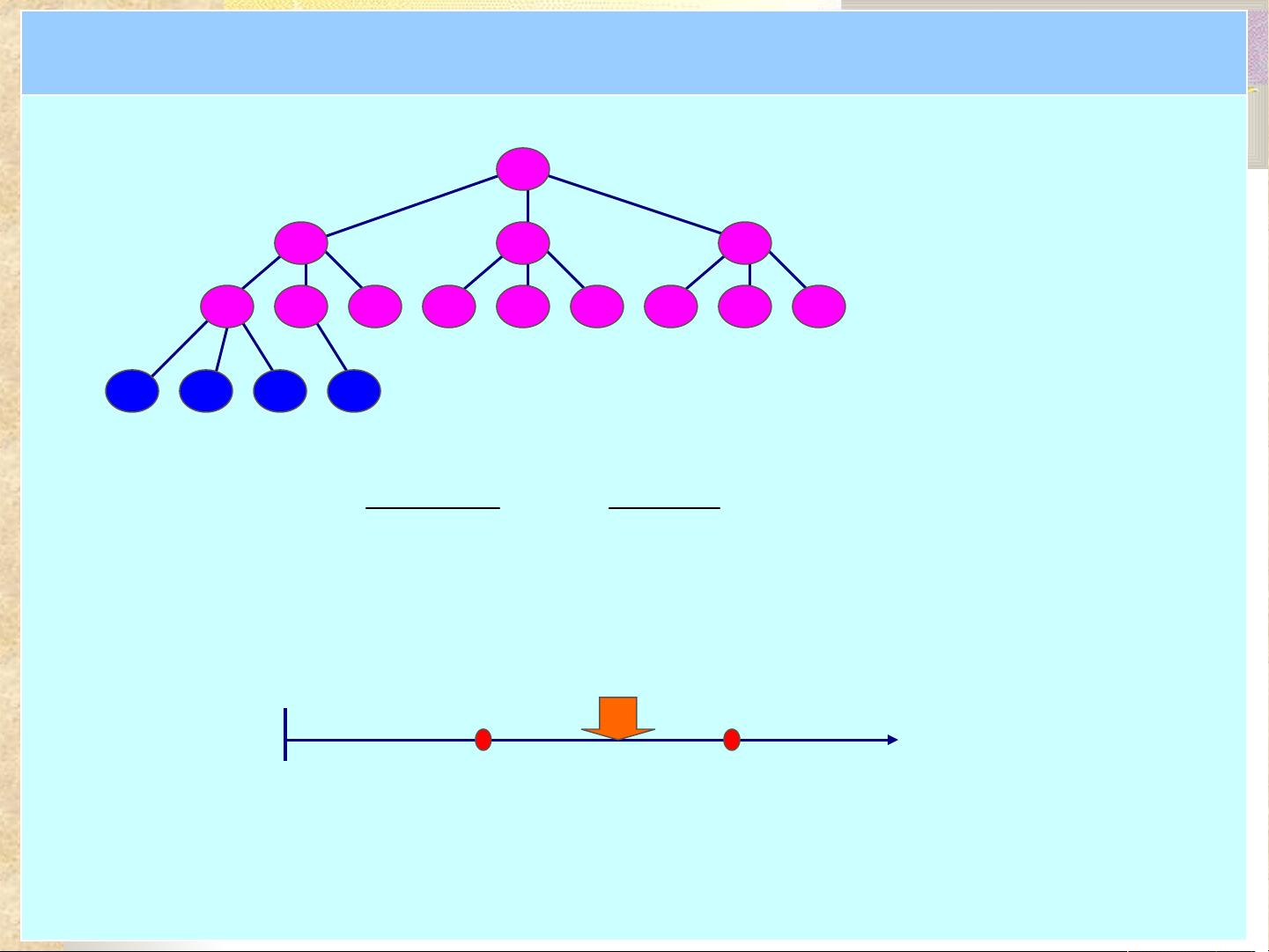
树的运算通常包括插入、删除、查找等操作。树的性质包括度(结点的子树数量)、高度(最远叶子结点到根的距离)、路径、路径长度、森林(由若干棵树组成的集合)等。
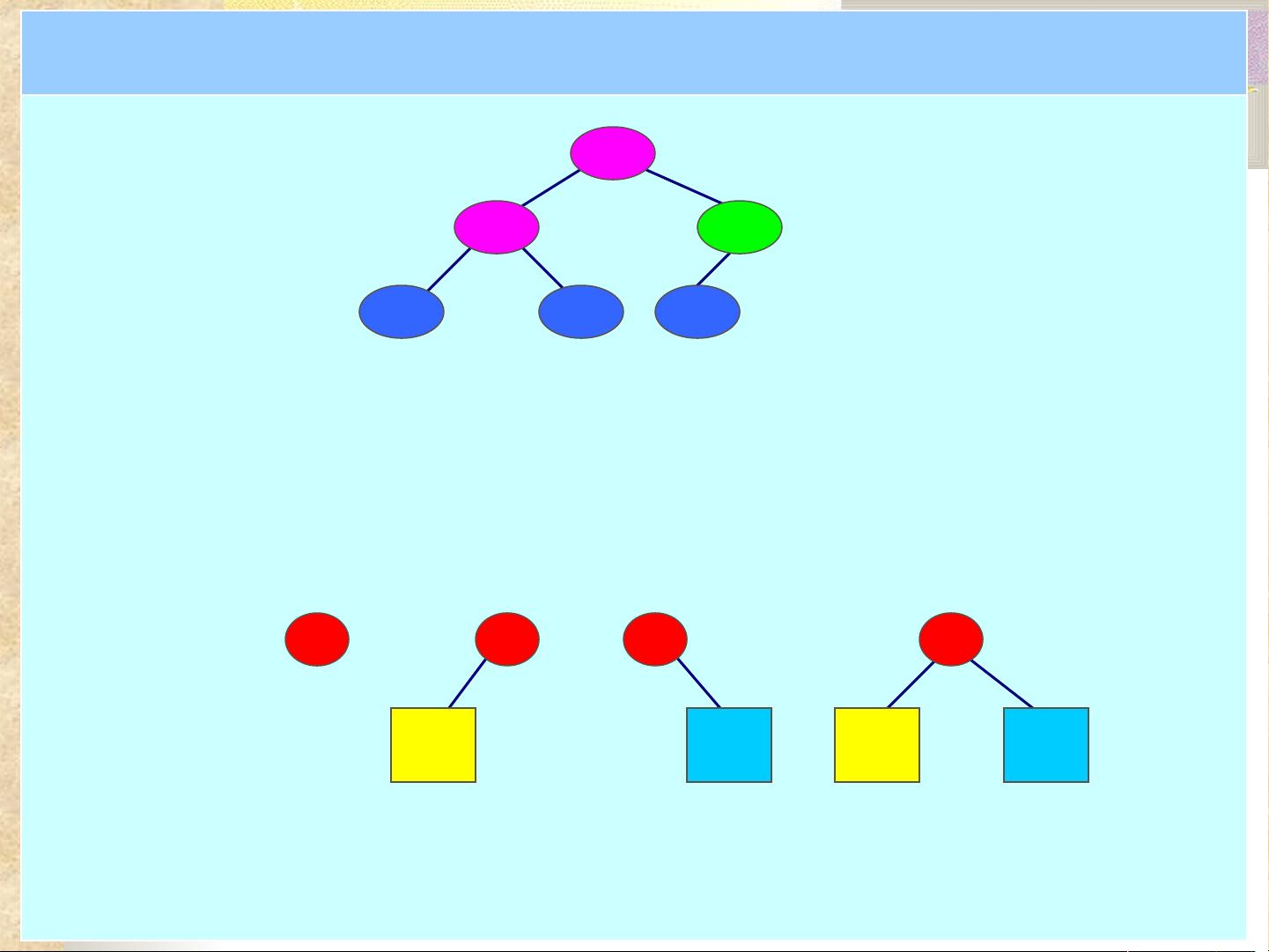
二叉树是特殊类型的树,每个结点最多有两个子结点,分为左子结点和右子结点。二叉树的遍历有三种方式:前序遍历(根-左-右),中序遍历(左-根-右)和后序遍历(左-右-根)。线索化二叉树是通过在二叉链表中增加线索来实现前序、中序和后序遍历的优化。
树与二叉树之间的转换是数据结构中一个有趣的话题,例如满二叉树和完全二叉树与普通树之间的转换。
此外,二叉树的一个经典应用是Huffman编码,这是一种用于数据压缩的编码方法,通过构建最优的二叉树(Huffman树),使得编码后的数据尽可能短,从而提高压缩效率。Huffman编码不仅用于文本压缩,还在其他领域有广泛应用。
理解并掌握树和二叉树的概念及其操作是学习数据结构的关键步骤,这对于后续学习算法和解决实际问题至关重要。这份课件提供了深入学习这一主题的良好资源,适合初学者逐步理解和掌握树的各个方面。
137 浏览量
2010-07-29 上传
705 浏览量
109 浏览量
2009-11-12 上传
2009-10-06 上传
2011-01-10 上传
105 浏览量
2009-08-23 上传
MariMari
- 粉丝: 0
- 资源: 3
最新资源
- 吉菲探索者
- 保险行业培训资料:地县级地区中端福寿连连销售逻辑
- frontend-react
- IEC101-103-104规约分析程序.rar
- 保险行业培训资料:从需求的角度看产品
- rms-list-gen
- DIU:乌苏里奥大学接口处
- tinyMCE:向 WordPress TinyMCE 添加自定义按钮
- 创维电视酷开系统14U系列8S26刷机应用工具包
- hex-to-rgb:将彩色十六进制值转换为rgb
- my-gridsome-app
- nexus-3.20.1-01-win64.rar
- nwis:对 nw.js GUI API 的 IntelliSense 支持
- materiaFramework:项目构建器,基于html POST请求
- IM Café-开源
- conquer_the_world:【打天下篇】工作知识纪要