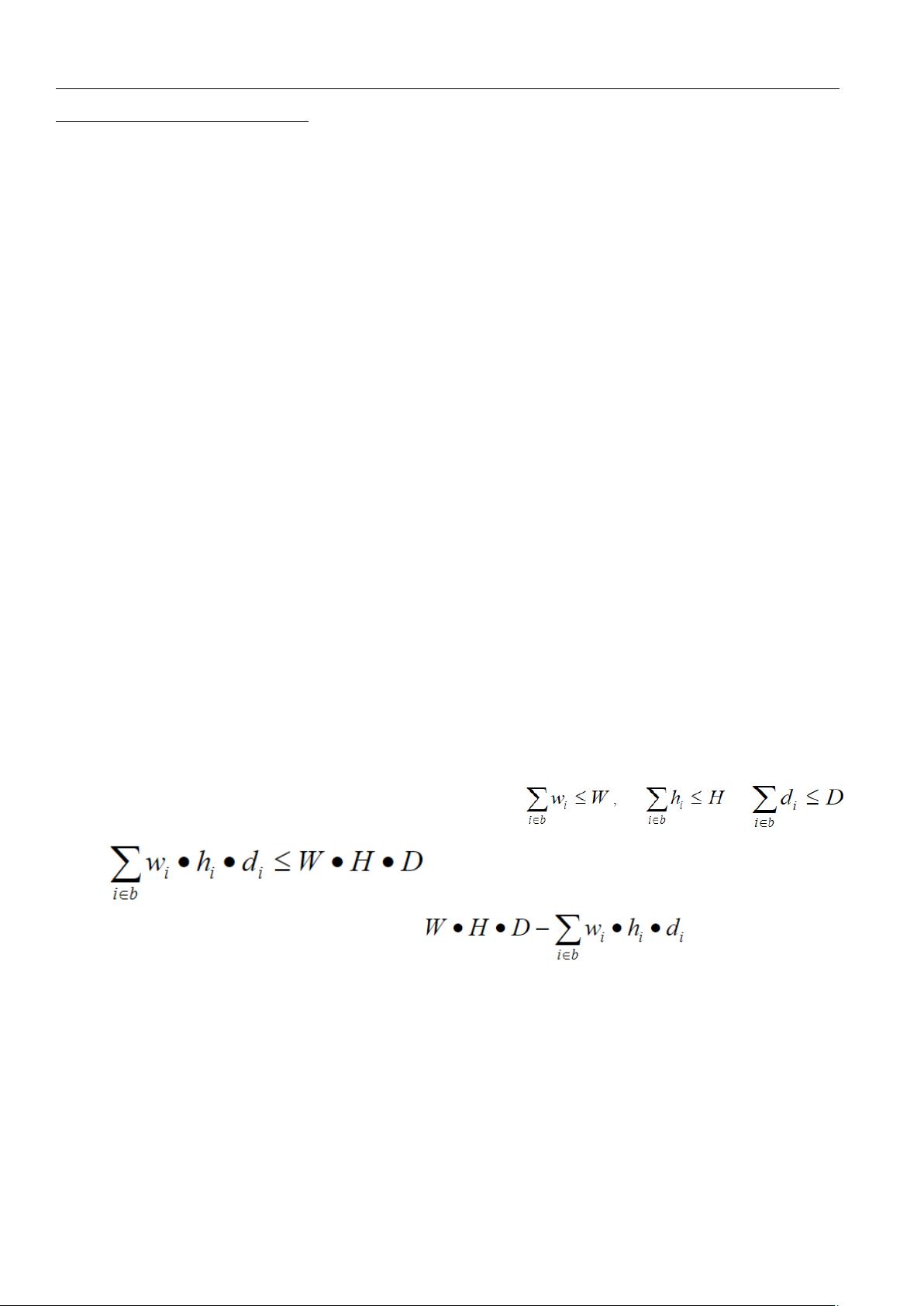通过仿真优化三维装箱问题

"通过仿真优化三维装箱(2006)\n本文解决的问题是将一组给定的矩形物品直接装入最少数量的三维矩形箱中。利用计算机的计算能力，采用启发式和背包问题的方法，以三维图形形式表示解决方案。关键词包括：仿真、优化、装箱、最佳适配、首次适配、旋转。文中介绍了一种模拟方法来构造和描述最优解的封装。此外，允许物品进行正交旋转以增加解决方案的多样性。虽然线性规划在一维问题中有应用，但在三维装箱问题中，由于其复杂性和NP-Hard性质，进化算法也被考虑，但它们的缺点是解决方案对问题参数变化敏感。因此，研究侧重于启发式方法，如FirstFit等，来寻找近似最优解。" 本文探讨了三维装箱问题的优化策略，其中目标是在保持一般性的前提下，为每个箱子b最小化冗余空间。这个问题是NP-Hard，意味着找到最优解在计算上是困难的。因此，作者提出了使用模拟方法，结合启发式算法和背包问题的策略来逼近最优解。 首先，问题定义为将一组具有宽度(wi)、高度(hi)和深度(di)的矩形物品装入具有固定尺寸W、H和d的三维箱子里。允许物品进行正交旋转，即交换宽度、高度和深度值，增加了解决方案的可能性。每个物品有6种不同的旋转配置，每种配置可能影响其与箱子的适应性。 在解决方案中，线性规划已被用于一维问题，但针对三维装箱问题，进化算法也被考虑。尽管进化算法能够探索大型搜索空间，但由于解与问题参数之间的连续性较差，当问题参数微小变动时，解决方案可能产生显著变化。因此，启发式算法，如FirstFit，成为更实际的选择。FirstFit策略是将未分配的物品放入第一个足够容纳它的箱子中，这种方法简单且适用于实时或计算资源有限的环境。 此外，文中提到的其他可能的启发式算法还包括BestFit，它将物品放入当前剩余空间最大的箱子，以及NextFit，每次尝试将新物品放入当前正在使用的箱子，如果无法容纳则开启新箱子。这些算法旨在在计算效率和解质量之间取得平衡。 这篇论文关注如何通过模拟和启发式算法来优化三维装箱问题，以在有限的计算资源下获得接近最优的解决方案。通过这种方法，即使在面对NP-Hard问题时，也能有效地解决实际装箱挑战。