拉普拉斯变换在信号与系统分析中的应用

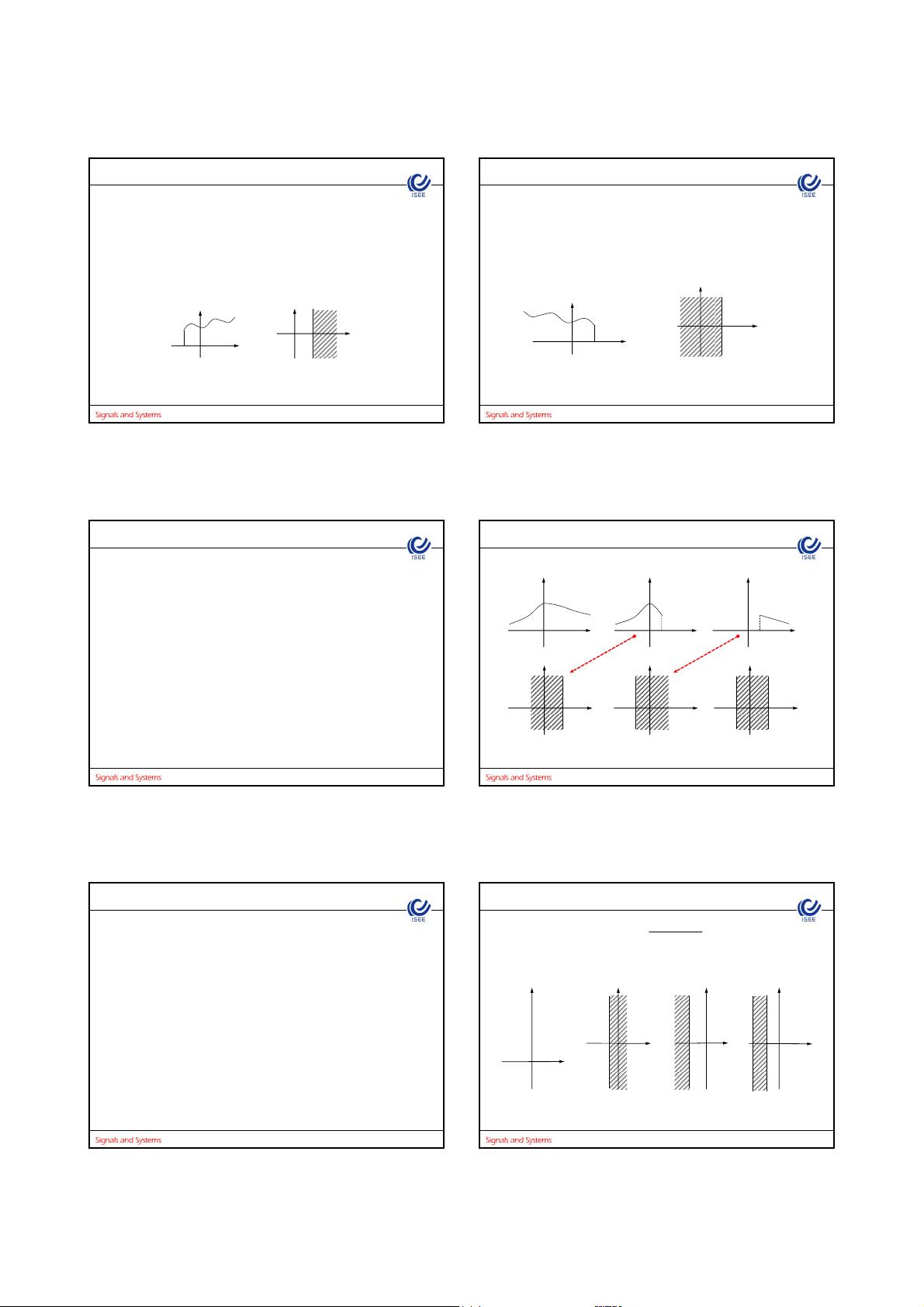
"浙大信号与系统第六章课件——复频域分析" 信号与系统是电子工程、通信、自动化等领域中的核心课程，其中第六章主要讲解的是信号与系统的复频域分析。复频域分析是一种利用拉普拉斯变换对连续时间信号和线性时不变（LTI）系统进行分析的方法，它可以扩展傅里叶变换的应用范围，解决一些傅里叶变换无法处理的问题，比如系统的稳定性分析。 拉普拉斯变换是傅里叶变换的一种推广，对于那些傅里叶变换不收敛或者计算复杂的信号，通过引入一个衰减因子e^(-σt)，可以使得更多的信号能够进行变换。这个衰减因子使得信号在时间域上随着t的增大或减小逐渐衰减，从而保证了变换的收敛性。拉普拉斯变换将信号从时间域转换到复频域，其中s = σ + jω，σ是实部，表示衰减常数，ω是虚部，对应于频率。 §6.1拉普拉斯变换介绍了拉普拉斯变换的概念，从傅里叶变换出发，解释了为何需要引入拉普拉斯变换以及其基本形式。拉普拉斯变换的定义是： X(s) = L{x(t)} = ∫_{-\infty}^{+\infty} x(t)e^{-st} dt 其中，X(s)是拉普拉斯变换后的函数，x(t)是原函数，s是复变量。 §6.2常用信号的拉普拉斯变换对则列举了一些常见信号的拉普拉斯变换，这些预知的变换对在实际问题中非常有用，可以帮助快速求解问题。 §6.3双边拉氏变换的性质讨论了拉普拉斯变换的一些基本性质，例如线性性质、时间平移、尺度变换等，这些性质使得在复频域内分析信号和系统变得相对简单。 §6.4周期信号与抽样信号的拉氏变换这部分内容会涉及如何处理周期性和抽样信号的拉普拉斯变换，这对于理解和处理实际工程中的信号至关重要，因为很多实际信号都是周期性的或经过抽样处理的。 §6.5拉氏反变换讲述了如何从复频域的X(s)反变换回时间域的x(t)，这对于解析系统的输出响应是必要的。通常会采用部分分式展开法或其他方法来求解。 §6.6单边拉氏变换及性质，单边拉普拉斯变换只考虑正时间区域的信号，适用于初始值为零的系统分析，它的性质和双边拉普拉斯变换有所不同。 最后，§6.7连续时间LTI系统的复频域分析利用拉普拉斯变换研究连续时间LTI系统的特性，如传递函数、频率响应等。通过系统函数H(s)，可以分析系统对各种输入信号的响应，包括稳定性、频率选择性等。 总结来说，这一章的内容涵盖了从基本的拉普拉斯变换概念，到其在处理各种类型信号和系统分析中的应用，对于理解和应用信号与系统的复频域理论具有重要意义。通过学习这一章，学生能够掌握如何利用复频域分析解决实际工程问题，为后续的控制系统设计、滤波器分析等高级主题打下坚实的基础。