Dijkstra算法详解：解决最短路径问题

"最短路问题及算法" 最短路问题是一个经典的图论问题，它在计算机科学和网络分析中有广泛的应用，例如在路由选择、交通规划和社交网络分析等领域。这个问题的目标是从一个指定的起点节点（源节点）到图中的其他所有节点找到具有最小总权重的路径。 Dijkstra算法是由荷兰计算机科学家Edsger Dijkstra在1956年提出的，它是解决单源最短路径问题的一种有效方法。在无权图或非负权重的图中，Dijkstra算法能保证找到从源节点到所有其他节点的最短路径。该算法基于贪心策略，每次扩展当前已知最短路径中最接近源节点的未访问节点。 Dijkstra算法的基本步骤如下： 1. 初始化：设置一个距离向量`l`，其中`l[i]`表示源节点到节点`i`的当前估计最短距离。初始时，`l[source] = 0`，其他节点的`l`值设为无穷大，表示没有找到路径。同时设置一个标志向量`z`，记录到达每个节点的前驱节点，`z[source] = source`。 2. 使用一个优先队列（通常用二叉堆实现）存储未访问的节点，按距离升序排列。 3. 在循环中，每次从优先队列中取出当前最短距离的节点`u`，然后检查其所有相邻节点`v`。如果通过`u`到达`v`的距离比当前已知的`l[v]`更短，就更新`l[v]`和`z[v]`。如果`v`还没有被访问过，就将其加入优先队列。 4. 重复第三步，直到优先队列为空，即所有节点都被访问过。 5. 最后，`l`向量包含了从源节点到所有节点的最短路径长度，而`z`向量则记录了最短路径上的中间节点。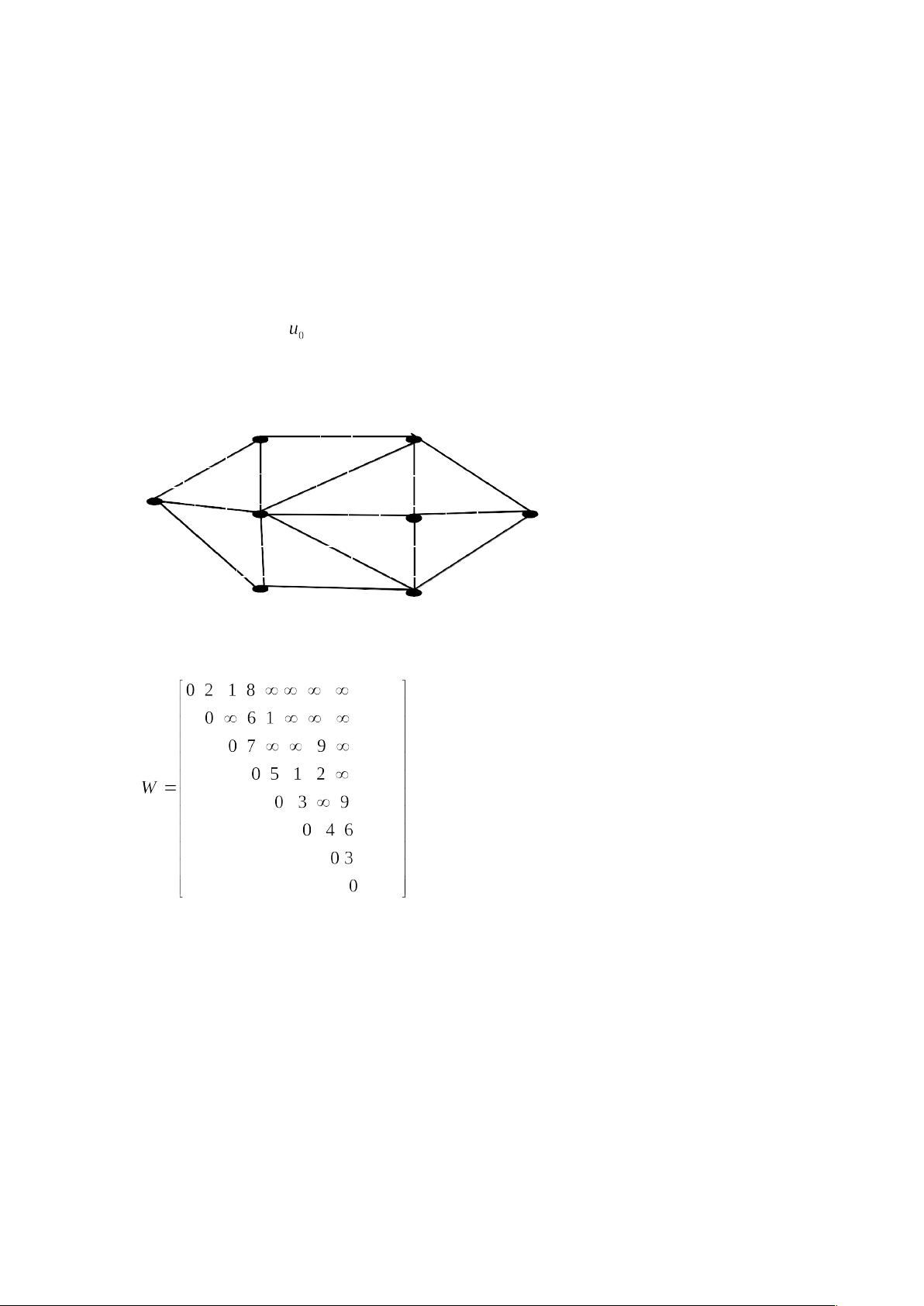 在MATLAB中实现Dijkstra算法，可以创建一个函数，输入是图的邻接矩阵`W`，输出是距离向量`l`和前驱节点向量`z`。给出的MATLAB代码示例中，`l`和`z`在遍历过程中不断更新，直到所有节点都被处理。 在实际应用中，Dijkstra算法存在局限性，它不能处理存在负权重边的图，因为这可能导致算法无法找到全局最优解。对于这种情形，可以使用其他算法，如Bellman-Ford算法或Floyd-Warshall算法。 总结来说，最短路径问题和Dijkstra算法是图论中的核心概念，它们在解决各种网络优化问题时发挥着关键作用。了解并熟练掌握这些算法，对于从事计算机科学，尤其是算法设计和分析的人员至关重要。