"数字信号处理：单位冲激与阶跃信号下的系统响应分析"

本实验的主要目的是熟悉连续LTI系统在单位冲激信号和单位阶跃信号下的系统单位冲激响应h(t)和阶跃响应g(t)，并掌握使用Matlab语言对线性系统进行描述和理解线性时不变系统的意义。此外，还要熟悉卷积的定义和表示，掌握使用卷积函数conv进行信号的卷积运算和可视化，并掌握使用卷积法计算LTI连续时间系统的求解法。 在本实验中，我们编写了一个Matlab程序来实现上述目标。程序中使用了方法1来计算系统的单位冲激响应h(n)和单位阶跃响应g(n)。具体的代码如下： ```Matlab a = [1,0,0,0,0,0,0]; b = [1,0,0,0,0,0,1]; N = 32; n = 0:N-1; hn = impz(b, a, n); % 求时域单位冲激响应 gn = dstep(b, a, n); % 求时域单位阶跃响应 subplot(1, 2, 1); stem(n, hn, 'k'); % 显示冲激响应曲线 title('单位冲激响应'); ylabel('h(n)'); xlabel('n'); axis([0,N,-1.1*min(hn),1.1*max(hn)]); subplot(1, 2, 2); stem(n, gn, 'k'); % 显示阶跃响应曲线 title('单位阶跃响应'); ylabel('g(n)'); xlabel('n'); axis([0,N,-1.1*min(gn),1.1*max(gn)]); ``` 在上面的代码中，我们定义了两个信号的差分方程（b和a），然后通过`impz`函数求解单位冲激响应h(n)，并通过`dstep`函数求解单位阶跃响应g(n)。接下来，在一个2x1的图像窗口中，我们使用`stem`函数分别绘制了冲激响应和阶跃响应的曲线，并添加了相应的标题和坐标标签。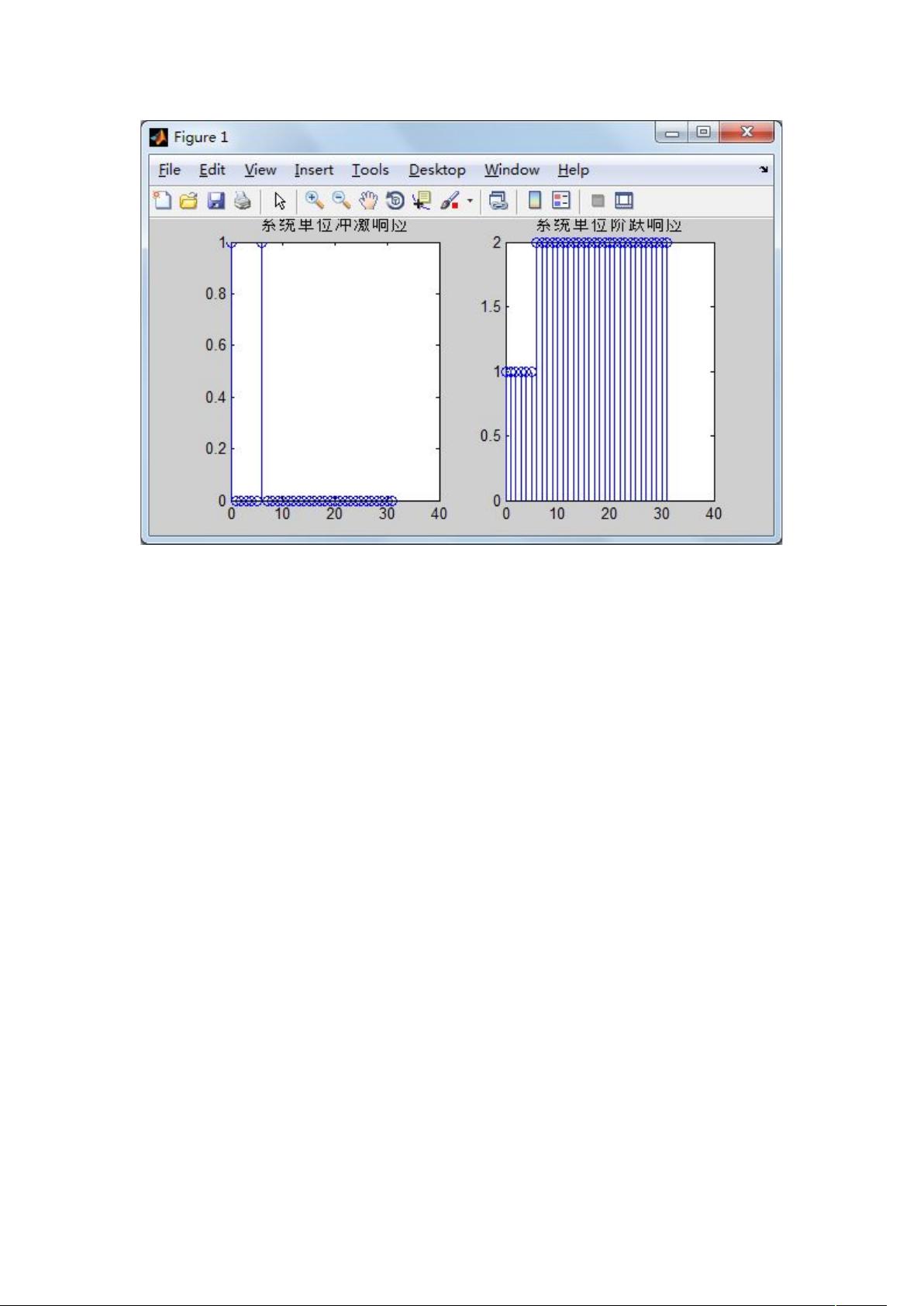 这段代码的运行结果如下图所示。其中，左侧的图像为单位冲激响应h(n)，右侧的图像为单位阶跃响应g(n)。 通过运行这段代码，我们可以观察到单位冲激响应和单位阶跃响应的形状和特点。从单位冲激响应可以得到系统的重要特性，如零极点位置，频率响应等；而单位阶跃响应则可以展示系统的稳态响应特性，如稳态增益、稳态误差等。 在本实验中，我们进一步理解了线性时不变系统的意义。线性时不变系统是实际系统中最常见的一类系统，其具有线性性质和时不变性质。线性性质指系统对输入信号的加权和具有线性关系，而时不变性质指系统的输出仅仅取决于当前的输入信号，而不考虑输入信号的时刻。这些特性使得线性时不变系统在信号处理中具有广泛应用。 此外，我们还学习了卷积的定义和表示，并掌握了使用卷积函数conv进行信号的卷积运算和可视化。卷积是一种重要的信号处理操作，用于描述输入信号和系统响应之间的非线性作用。卷积运算可以帮助我们理解信号在系统中的传输和变换过程。 总之，通过本实验，我们深入学习了数字信号处理中的单位冲激响应、单位阶跃响应和卷积操作。这些知识对我们理解和应用数字信号处理技术具有重要意义，为我们进一步研究和应用相关领域奠定了基础。