J. Zhang et al. Journal of Network and Computer Applications 124 (2018) 108–120
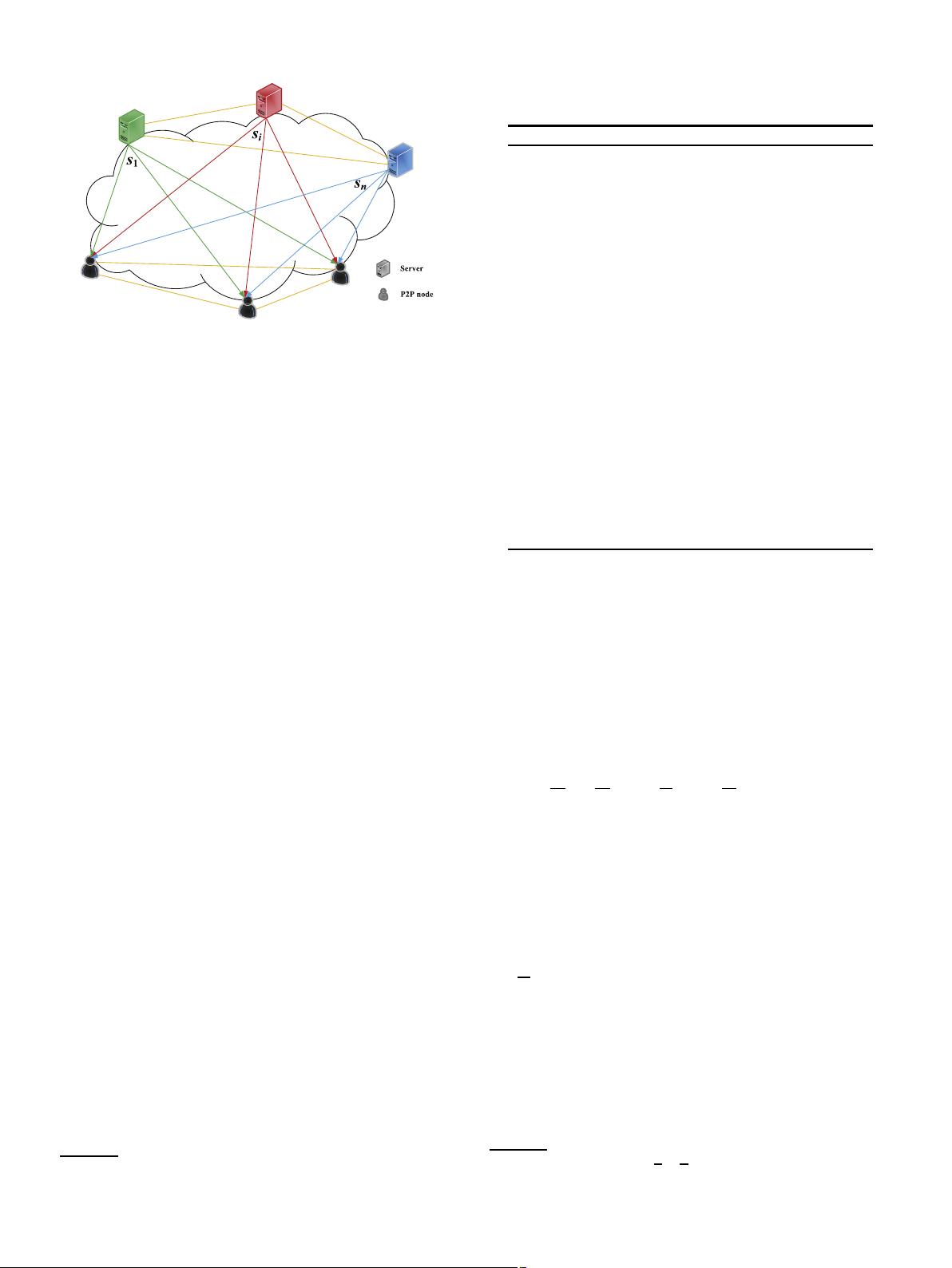
Fig. 1. System model. There are two networks: the server network and the P2P
network. Every server multicasts its own stream to the whole P2P network.
service in geographically distributed datacenters. They take full advan-
tages of the SDN architecture to obtain centralized online scheduling
solutions, which can fully exploit the spare inter-datacenter bandwidth.
Ishakian et al. (2017) build a cloud-based service AngelCast which can
assist streaming service providers in delivering quality streams to P2P
nodes, while making the best use of P2P bandwidth. Noteably, they also
present the notion of angels, a group of helper servers assigned to for-
ward only a part of the streams, which shares some common features
with our work.
Although the above works seem not theoretically relevant to this
paper, they offer reference and experience in how to adapt the pro-
posed approach to emerging networking paradigms, such as datacenter
networks and software-defined networks (SDNs).
3. System overview
3.1. Problem formulation
In Fig. 1, there are two networks: the server network and the P2P
network. The server network consists of n servers, each of which has a
distinct stream s
i
andanuploadbandwidthC
i
. The P2P network consists
of N P2P nodes, with a total upload bandwidth U. Every server wants
to multicast its own stream to all P2P nodes. The main notations in this
paper are listed in Table 1.
In this paper, we make the following assumptions unless mentioned
otherwise. These assumptions are consistent with the works using flow-
based models (Mehyar et al., 2007; Ezovski et al., 2009; Kumar and
Ross, 2006; Kumar et al., 2007; Meng et al., 2013; Meng, 2013).
• The system is free of node churn. For the considered problem, a
static scenario can provide useful insights and is a starting point for
a more complex dynamic scenario.
• All servers and all P2P nodes constitute a fully-connected network;
thus, the numbers of connections within the servers, within the P2P
nodes, and between the two networks are unlimited.
• Streams can be divided into infinitesimal chunks. A server or P2P
node can immediately relay what it receives to another server or
P2P node. Thus, there is no forwarding delay.
• The upload bandwidth, instead of the download bandwidth, is the
bottleneck, because edge nodes usually have asymmetric Internet
access, and the backbone usually has an abundant bandwidth.
2
• Network coding is not allowed at servers or P2P nodes, because
the encoding and decoding operations will introduce considerable
computation cost and delay.
2
In the following, the term bandwidth refers to upload bandwidth unless oth-
erwise mentioned.
Table 1
Notations.
Notation Description
n Total number of servers.
N Total number of P2P nodes.
C
i
Upload bandwidth of server i.
f
i,j
Upload bandwidth of server i used for s
j
.
p
i
Upload bandwidth of P2P node i.
p
i,j
Upload bandwidth of P2P node i used for s
j
.
U Total upload bandwidth of the P2P network.
U
i
Total upload bandwidth allocated to s
i
in the P2P network.
𝜃
i
Relative streaming rate of s
i
.
𝜃 Maximum achievable relative streaming rate of all streams.
𝜃
max
Maximum allowable relative streaming rate for all streams.
s
i
Stream i, which originates from server i.
r
0
i
Original streaming rate of s
i
,seeEq.(1).
r
1
i
Maximum achievable streaming rate of s
i
,seeEq.(24).
r
2
i
Maximum possible streaming rate of s
i
,seeEq.(21).
r
3
i
Maximum allowable streaming rate of s
i
,seeEq.(23).
s
′
i
Virtual stream i, consisting of s
i
, s
i+1
, … , s
n
.
R
0
i
Original streaming rate of s
′
i
,seeEq.(28).
R
1
i
Maximum achievable streaming rate of s
′
i
,seeEq.(31).
R
2
i
Maximum possible streaming rate of s
′
i
,seeEq.(29).
R
3
i
Maximum allowable streaming rate of s
′
i
,seeEq.(28).
LP Linear program(ming).
LS Linear system.
TUB Theoretical upper bound.
TLB Theoretical lower bound.
OF Optimal forwarding strategy.
ONF Optimal non-forwarding strategy.
WF Water-filling algorithm.
From a practical perspective, the considered model under these
assumptions can be applied to the promising datacenter networks
(DCNs). Among various types of architecture and topology (Bari et al.,
2013), the servers in many of them can be interconnected in a fully-
connected P2P manner, e.g., Dcell (Guo et al., 2008), VICTOR (Hao et
al., 2009), SEC2 (Hao et al., 2010), Jetway (Feng et al., 2012a)and
Airlift (Feng et al., 2012b).
The original streaming rate and achievable streaming rate of s
i
are
denoted by r
0
i
and r
1
i
, respectively. Without loss of generality,
3
we
assume that the original streaming rates and upload bandwidths of all
servers satisfy:
𝜃
max
∶=
C
1
r
0
1
<
C
2
r
0
2
< … <
C
i
r
0
i
< … <
C
n
r
0
n
, (1)
where
𝜃
max
is defined as the maximum allowable relative streaming rate
for all streams.
As such, all servers are ordered sequentially according to their ser-
vice capabilities. The server with larger index can provide larger per-
centage of its bandwidth to help forward other streams. In practice,
server i can be deployed using multiple servers containing the same
stream s
i
. Their upload bandwidths are not necessarily equal.
Define the relative streaming rate of s
i
as:
𝜃
i
=
r
1
i
r
0
i
, i ∈[1, n]. (2)
Suppose all the streams are of equal importance, the objective of this
paper is to maximize the relative streaming rates of multiple streams
while keeping them synchronized, which is referred to as multi-stream
live streaming problem. Conceptually, we have:
(P) max 𝜃
s.t.𝜃
i
= 𝜃, i ∈[1, n]. (3)
3
Note that if for some i and j,
C
i
r
0
i
=
C
j
r
0
j
, then the two servers can be considered
a single virtual server. Hence, we omitted this trivial case in Eq. (1).
110









