图解大顶堆与堆排序详解
166 浏览量
更新于2024-08-30
收藏 510KB PDF 举报
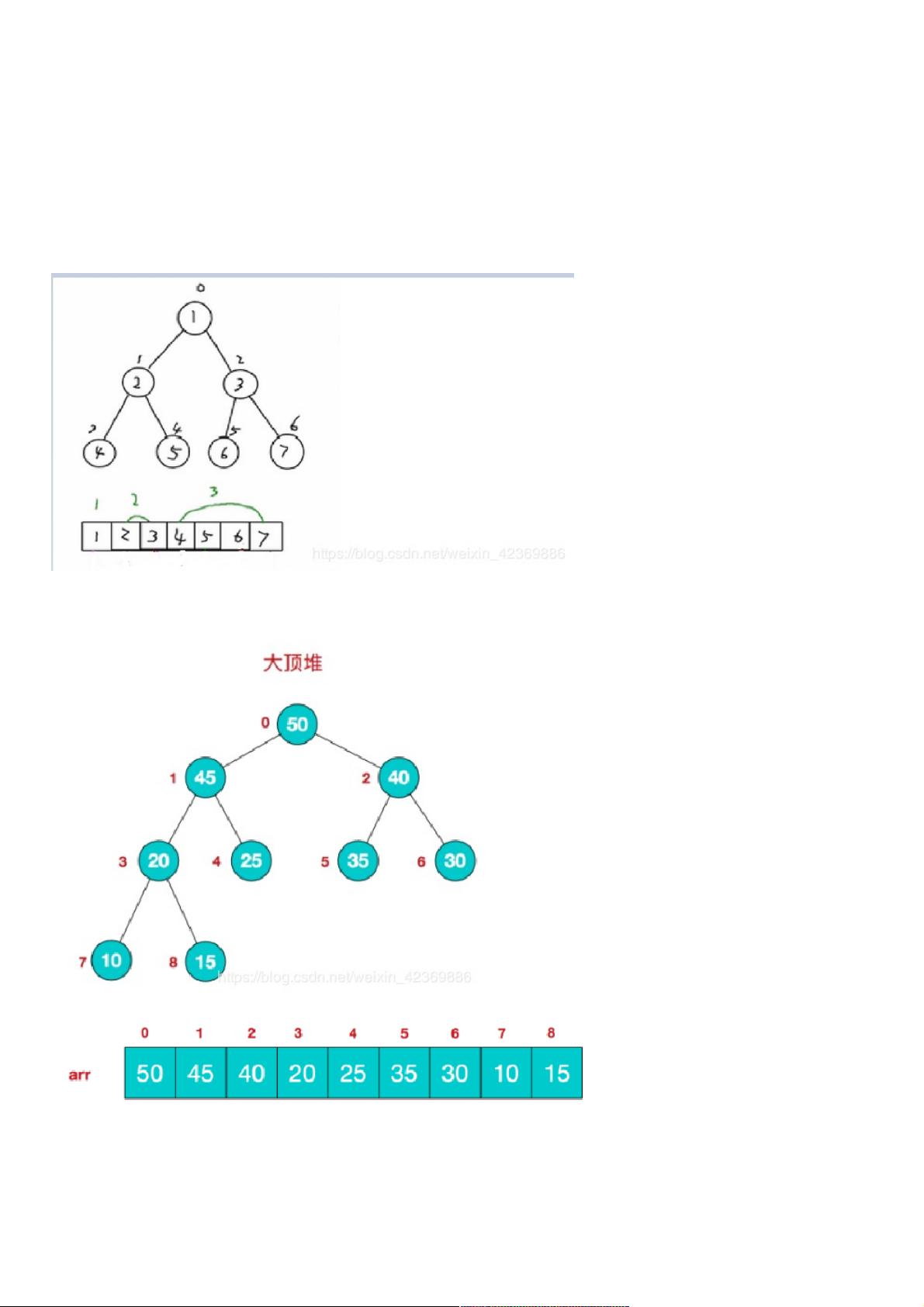
堆排序是一种基于比较的排序算法,它利用了堆这种数据结构来进行操作。在进行排序前,了解顺序存储二叉树和堆的概念至关重要。顺序存储二叉树是指通过数组方式存储二叉树节点,强调的是完全二叉树的特性,其中节点间的父子、兄弟关系可以通过简单的数学公式计算得出。堆则分为大顶堆和小顶堆,大顶堆的特点是每个节点的值大于或等于其左右孩子的值,而小顶堆则相反,每个节点的值小于或等于其左右孩子的值。
堆排序的基本原理如下:
1. **构建堆**:首先将待排序序列构建成一个大顶堆(升序排序时使用),这样序列的最大值位于堆顶。
2. **交换和调整**:每次取出堆顶元素(最大值),与序列末尾元素交换位置,然后调整剩余部分,使之再次成为大顶堆。重复此过程,直至整个序列有序。
对于给定的无序序列{4,6,8,5,9},堆排序的步骤包括:
- **初始化**:无序序列作为堆。
- **调整堆**:从最后一个非叶子节点开始,逐级向上调整,确保每个子树都是大顶堆。
- **交换**:将堆顶元素与末尾元素交换,保证最大元素移到序列末尾。
- **重复调整**:对剩余元素重新构建堆,找到次大元素并交换,重复此过程,直到序列完全有序。
堆排序的代码实现通常涉及一个名为`buildMaxHeap`的方法来构建堆,以及`heapify`或`swapAndHeapify`等辅助函数来维护堆的性质。以下是Java中的一个简化版堆排序实现:
```java
public class HeapSort {
public static void heapify(int arr[], int n, int i) {
int largest = i; // 初始化最大元素索引为i
int left = 2 * i + 1; // 左子节点索引
int right = 2 * i + 2; // 右子节点索引
// 如果左子节点比当前元素大,则更新最大元素索引
if (left < n && arr[left] > arr[largest]) {
largest = left;
}
// 如果右子节点比当前最大元素大,则更新最大元素索引
if (right < n && arr[right] > arr[largest]) {
largest = right;
}
// 如果最大元素不是当前节点,交换它们的位置,并递归地调整子树
if (largest != i) {
swap(arr, i, largest);
heapify(arr, n, largest);
}
}
public static void sort(int arr[]) {
int n = arr.length;
// 构建大顶堆
for (int i = n / 2 - 1; i >= 0; i--) {
heapify(arr, n, i);
}
// 依次将堆顶元素与末尾元素交换,然后调整堆
for (int i = n - 1; i > 0; i--) {
swap(arr, 0, i);
heapify(arr, i, 0);
}
}
// 交换数组中的两个元素
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
public static void main(String[] args) {
int arr[] = {4, 6, 8, 5, 9};
sort(arr);
System.out.println("Sorted array: ");
for (int num : arr) {
System.out.print(num + " ");
}
}
}
```
通过以上步骤,堆排序能够有效地对给定数组进行升序排序,同时保持时间复杂度为O(n log n),空间复杂度为O(1)。
2024-09-30 上传
2024-09-26 上传
点击了解资源详情
点击了解资源详情
2013-12-18 上传
2022-04-07 上传
2021-09-07 上传
2018-03-30 上传
2021-09-10 上传
weixin_38672807
- 粉丝: 9
- 资源: 923
最新资源
- 基于深度神经网络的DST指数预测.zip
- webpage
- 行业文档-设计装置-一种利用余热烘烤纸管的装置.zip
- word-frequency:小型javascript(节点)应用程序,该应用程序读取文本文件,并按顺序输出文件中20个最常用的单词以及它们的出现频率
- dltmatlab代码-dlt:用于计算离散勒让德变换(DLT)的MATLAB代码
- php-subprocess-example:使用Symfony Process Component和异步php执行的示例
- quick-Status
- .....
- 基于webpack的前后端分离方案.zip
- crossword-composer:文字游戏的约束求解器
- 电力设备与新能源行业新能源车产业链分析:_电动化持续推进,Q1有望淡季不淡.rar
- UnraidScripts
- dltmatlab代码-DLT:http://winsty.net/dlt.html
- ant.tmbundle:TextMate对Ant的支持
- zhaw-ba-online
- CandyMachineClient