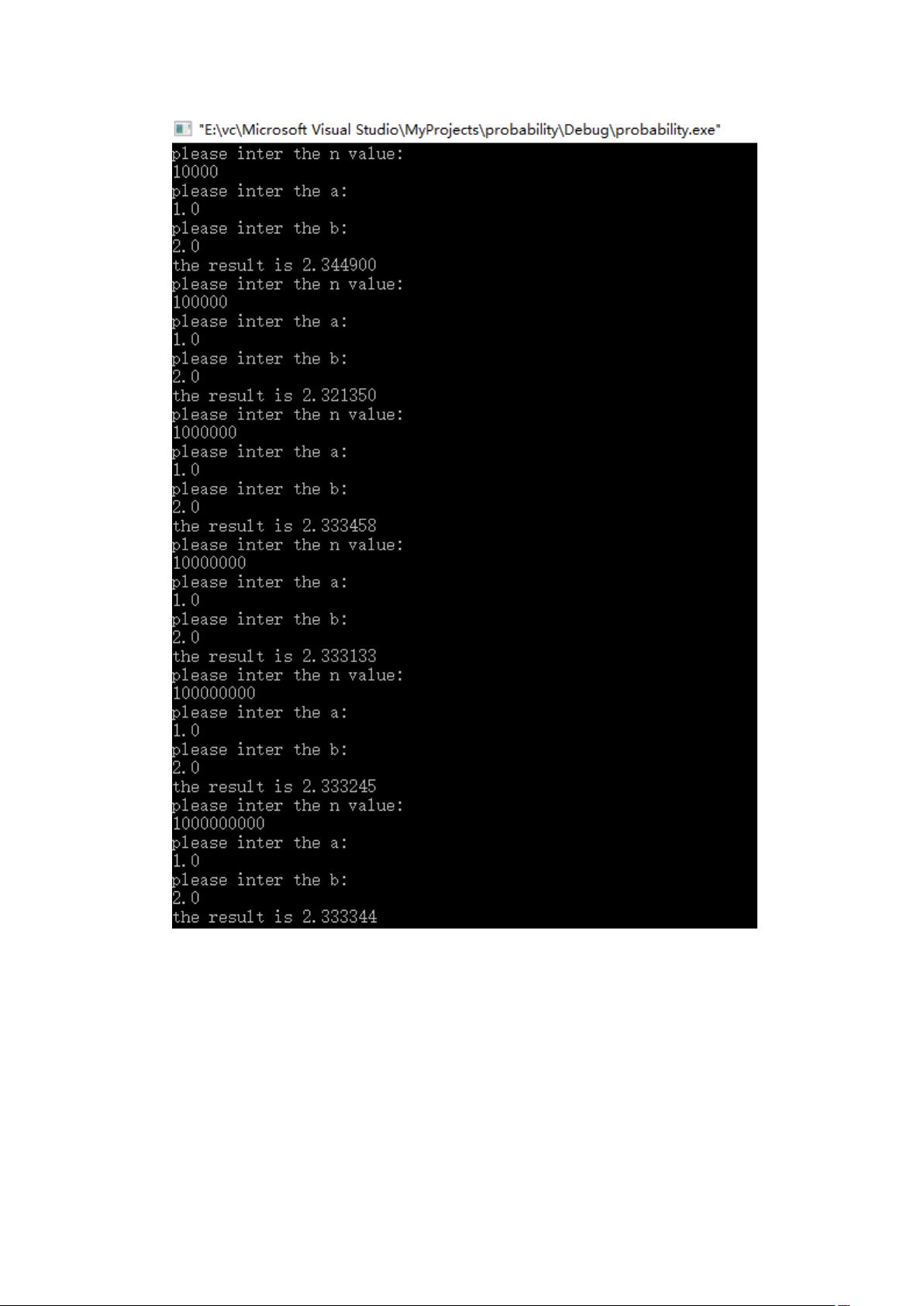
"单位圆内的点分布及长度估计概率算法1与Ex1比较"
需积分: 0 14 浏览量
更新于2024-03-21
收藏 108KB DOCX 举报
在概率算法1中,首先考虑到点(x, y)满足条件x*x + y*y <= 1,因此这些点位于单位圆内。同时,由于y = x,这些点也分布在直线y = x上。根据这些特性,我们可以将算法简化为求解直线y = x在单位圆内的长度与在单位正方形内的长度的比值的四倍。
在进行数值计算时,我们将原先的y < -uniform(0, 1)替换为y = x,即y = x。这会导致算法估计的值变为y = x在单位圆内的长度与在单位正方形内的长度的比值的四倍。具体来说,这个比值是2√2 / 1 * 4 = 8√2。
在执行算法后,我们发现结果符合预期。具体代码如下:
```c
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main() {
int num_points = 100000; // 生成的点数
int count_circle = 0; // 单位圆内的点数
int count_square = 0; // 单位正方形内的点数
for (int i = 0; i < num_points; i++) {
double x = drand48(); // 生成0~1间的随机数作为x坐标
double y = x; // y = x
count_square++; // 在单位正方形内的点数自增
if (x*x + y*y <= 1) {
count_circle++; // 在单位圆内的点数自增
}
}
double ratio = (double)count_circle / count_square * 4; // 比值计算
printf("估计的比值为: %f\n", ratio);
return 0;
}
```
通过这段代码,我们可以实现对y = x在单位圆内的长度与在单位正方形内的长度的比值的估计。这个例子展示了如何通过概率算法来进行数值计算,并通过代码实现这一过程。
2022-08-08 上传
2022-08-08 上传
2022-08-04 上传
2022-08-04 上传
2022-08-08 上传
2022-08-04 上传
2022-05-17 上传
王元祺
- 粉丝: 848
- 资源: 303
最新资源
- Flex 3 Cookbook简体中文.pdf
- <程序员的SQL金典>
- 嵌入式linux开发手册
- SD卡接口规范的完整翻译
- Oracle10g_DBA..
- JCreator配置JSP环境方法
- MYSQL DBA 必读 understanding mysql internals
- 理解 ASP3.5.NET 基础结构.pdf
- 嵌入式系统原理,设计与应用
- AT89S51+单片机实验及实践教程
- ClearCase 客户端使用指南.pdf
- C++ GUI Programming with Qt 4, Second Edition
- 正则表达式常用正则表达式收集
- 家庭理财系统的可行性研究
- IT服务管理 基于ITIL的全球最佳实践
- jdbc api数据库编程实作教材