频域仿真建模方法：从S域到Z域的转换

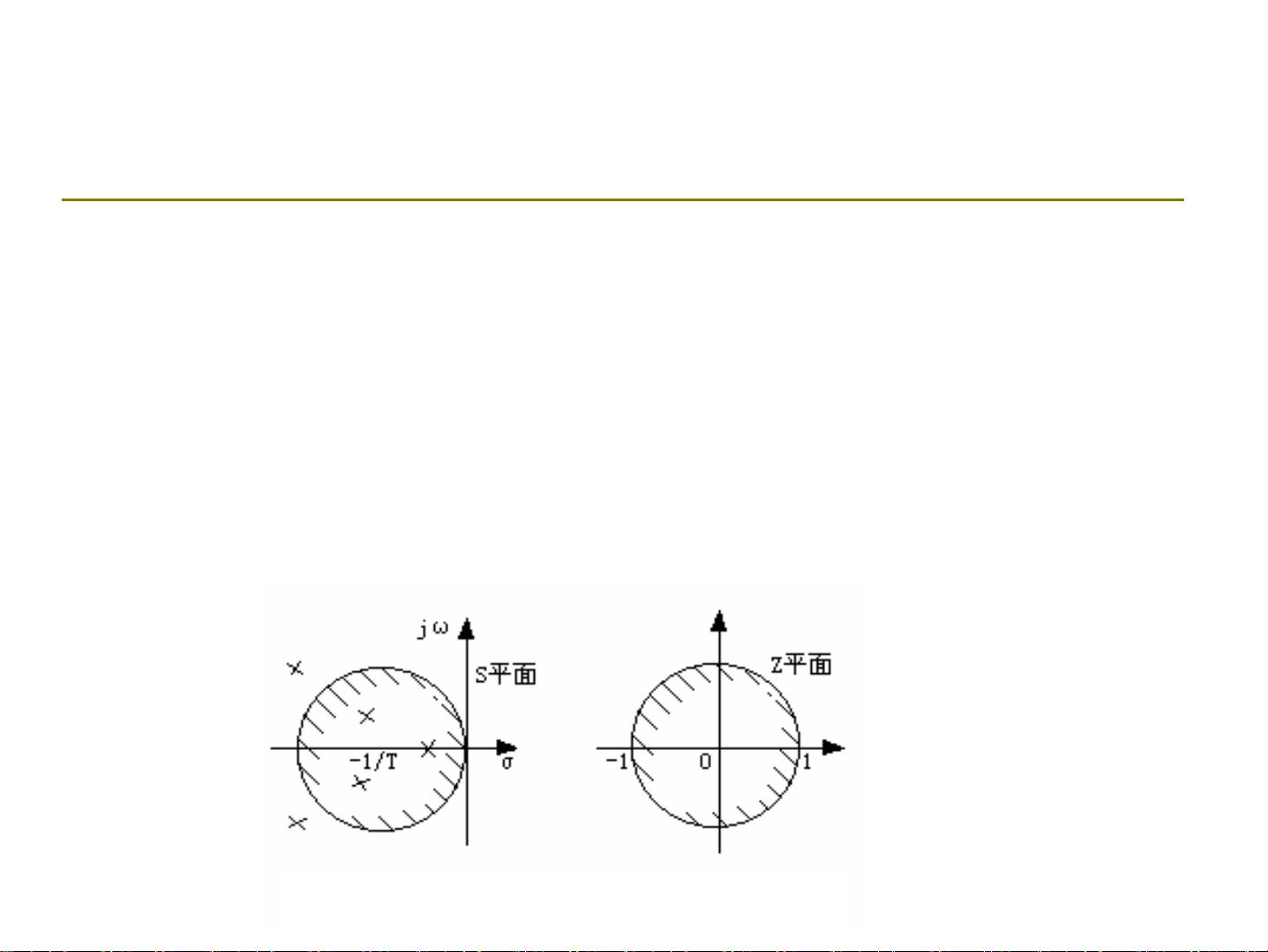
"系统仿真技术_Chapter 4 频域仿真建模方法学.pdf" 频域仿真建模方法是系统仿真中的一个重要分支，主要应用于控制系统的分析和设计。本章节聚焦于频域仿真，即在复频域内进行系统建模和分析。这种方法特别适合处理线性时不变系统，如在通信、自动化和航空航天等领域广泛应用。 首先，频域仿真基于传递函数的概念，传递函数是系统动态特性的频率表示，通常以复变量s（拉普拉斯变换变量）为自变量。对于给定的控制系统，可以用常微分方程、传递函数或状态空间描述来表示。例如，描述控制系统动态行为的方程式可能包含输入u、输出y以及内部状态变量c和a。这些方程可以通过拉普拉斯变换转换到S域，得到传递函数G(s)。 然后，为了在计算机上求解这些模型，有两种主要的方法。第一种是数值积分法，通过数值方法解决常微分方程，比如欧拉法、龙格-库塔法等。这种方法适用于连续时间模型，但可能需要复杂的算法和较高的计算资源。第二种方法是离散时间模型，它将连续时间系统转换为离散时间模型，更适合计算机程序化求解。离散相似化包括时域离散相似化和频域离散相似化，其中时域离散相似化是将连续时间响应转换为离散时间响应，而频域离散相似化则涉及将传递函数从S域转换到Z域。 在频域内，系统响应可以通过其脉冲传递函数（PTF）来分析。PTF 描述了系统对单位阶跃输入的响应，是传递函数在z域的另一种形式。通过将传递函数G(s)变换为G(z)，我们可以得到与之对应的离散时间系统，这在数字信号处理和数字控制中至关重要。这个转换通常通过Z变换实现，目的是在离散时间环境下保持系统性能的近似等效。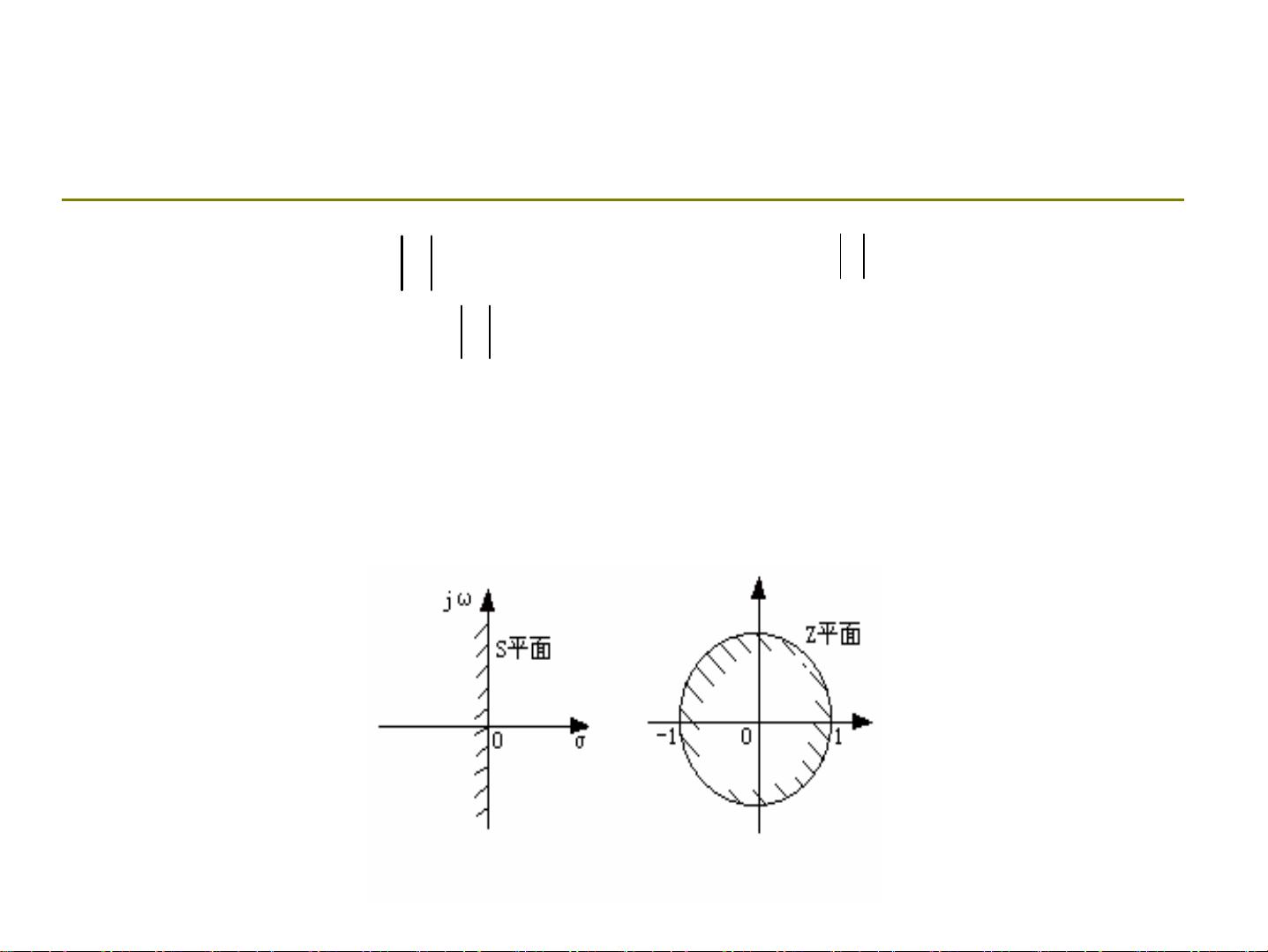 频域仿真建模方法的核心在于将S域的传递函数G(s)映射到Z域的传递函数G(z)。这一过程称为离散化，通过离散化，可以利用数字计算机进行数值计算和模拟。Z变换是此过程的关键工具，它允许我们将连续时间系统的特性转化为离散时间系统的特性，从而便于在计算机上进行计算和分析。 频域仿真建模方法提供了一种在频域内理解和设计系统的方法，尤其适用于线性系统的分析。通过传递函数和脉冲传递函数的处理，我们可以有效地将连续时间系统转换为离散时间系统，为实际的计算机仿真和数字控制设计提供基础。在工程实践中，这种方法被广泛用于预测系统性能，优化控制器参数，以及解决实际系统中的稳定性问题。