基于Bouguer-Beer定律的太阳光谱仪新型校准方法

43 浏览量更新于2024-08-27 收藏 224KB PDF 举报

"一种基于Bouguer-Beer定律的新太阳光度计校准方法被提出。这种方法的基础方程使得能够根据光学空气质量比的整数倍的光度测量来制定校准的导出方法。该研究涉及到010.0010、120.0120、280.0280和300.0300等特定光学频率代码，并引用了doi:10.3788/COL20090709.0760。" 新方法的提出是为了应对日益增长的空间和地面遥感设备的需求，这些设备对传感器的校准精度提出了更高的要求。传统的太阳光度计校准方法，如Langley图法，一直被视为地面设置太阳光度计的主要校准手段。Langley图法的核心是Bouguer-Beer定律，它阐述了太阳辐射强度在光谱中随大气光学厚度的增加而指数衰减的关系。 Bouguer-Beer定律，也被称为比尔-朗伯定律，指出通过物质（如大气）的辐射强度I(λ)与入射辐射强度I0(λ)和该物质的光学厚度mτatm之间的关系为指数函数形式，即I(λ)=I0(λ)e^(-mτatm)。这里的m是光学路径长度，τatm是单位长度的大气吸收系数。这个定律在遥感、天文学和环境科学等领域具有广泛的应用，特别是在理解和量化大气对太阳辐射的吸收和散射效应上。文章提到的新方法扩展了这一基本原理，提出了基于光学空气质量比的整数倍进行校准的衍生方法。光学空气质量（Optical Air Mass，m）是指太阳光线穿过大气层的路径长度与在海平面上垂直于地表路径长度之比，它影响了太阳辐射到达地面时的衰减程度。通过这种方法，可以更精确地调整和校准太阳光度计，提高其测量结果的准确性和可靠性。此研究可能对天文学、气候学、大气科学以及地球观测等领域有着重要的影响，因为它提供了一种改进现有校准技术的途径，有助于获取更准确的太阳辐射数据，从而更好地理解大气成分、气候变化以及地球的能量平衡。此外，这种方法还可能降低对复杂和昂贵的Langley图法的依赖，简化校准过程，提高效率。

760 CHINESE OPTICS LETTERS / Vol. 7, No. 9 / September 10, 2009

New method for calibration of sun photometers

H. H. Asadov

∗

and I. G. Chobanzadeh

Azerbaijan National Aerospace Agency, AZ1106, Av. Azadlig, Baku, Azerbaijan

∗

E-mail: hasadzade2001@yahoo.com

Received December 31, 2008

A new method for calibration of sun photometers based on Bouguer-Beer law is proposed. The developed

basic equation of calibration makes it possible to formulate the derivative methods of calibration on the

basis of photometric measurements upon optical air masses, the ratio of which is an integer number.

OCIS codes: 010.0010, 120.0120, 280.0280, 300.0300.

doi: 10.3788/COL20090709.0760.

It is obvious that the development of new space and

ground remote sensing device s leads to the increase of

requirements for more perfect calibration of these sen-

sors. One can state that till now the method of Langley

diagrams remains as a basic method for the calibration

of gr ound sets of sun photometers

[1−4]

. This method is

based on Boug uer-Beer law, a ccording to which the in-

tensity of solar radiatio n at the input of photometer I(λ)

may be determined as

I(λ) = I

(λ)e

−mτ

atm

, (1)

where λ is the wavelength, I

(λ) is the solar constant,

i.e., the intensity of sun radiation at the upper bo rder of

atmosphere; m is the optical air mass; τ

atm

is the optical

thickness of atmosphere, which is deﬁned in ultraviolet

(UV) band as

atm

= τ

+ τ

Ray

+ τ

aer

, (2)

where τ

, τ

Ray

, and τ

aer

are optical thicknesses of a tmo-

spheric ozone, Rayleigh scattering, and aerosol, respec-

tively.

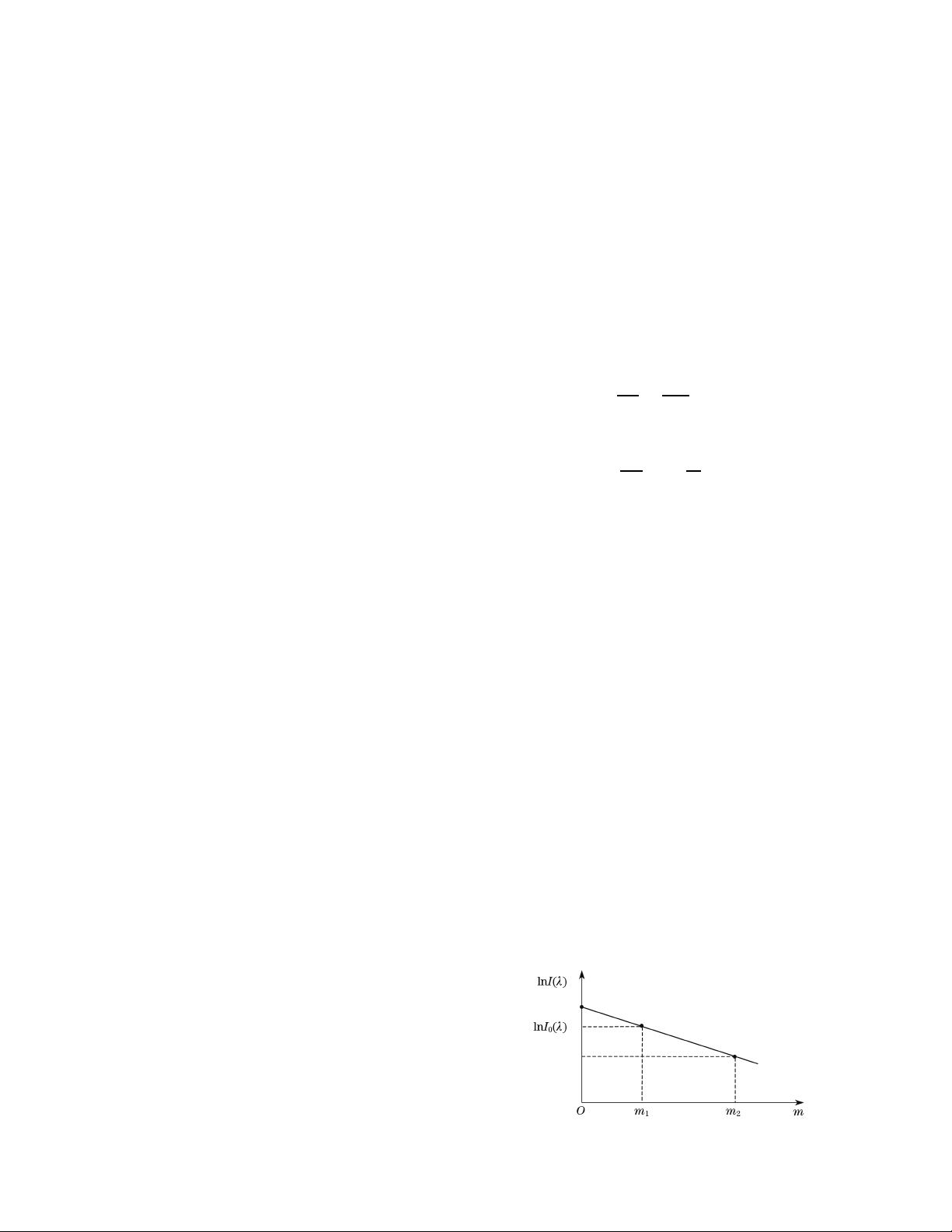
According to the method of Lang ley, Eq. (1) should be

transformed to

lnI(λ) = lnI

(λ) − mτ

. (3)

Then we can draw the linear diagram of dependence of

lnI(λ) on m, as shown in Fig. 1.

The common rule for drawing Langley diagrams con-

sists of the following steps.

1) Calcula tion of lnI(λ) for two values of m, i.e., m

and m

, which correspond to appropriate angles of ob-

serva tion of the Sun, θ

and θ

2) Drawing the graphic model of function lnI(λ) =

f(m) using two values of m.

3) The linear type graphics of afo resaid function is ex-

trapolated as far as m = 0, where this line crosses the

ordinate axis.

4) Taking into co ns ideration the linearity of “input-

output” functional dependence of the photometer. It

should be as sumed that the output sig nal is proportional

to I

(λ).

The main shortage of the Langley diagram method is

that temporal variations of optica l depth of atmosphere

may lead to mistakes in the calibration of photometers.

There are some modiﬁcations of this method. For exam-

ple, it is propos e d to use the fo rmula

[5]

lnI

− τ,

i.e., to draw simila r diagrams of

lnI

= f





It is stated that in the case of “shor t” diagrams

max

= 3), the Langley method and the alternative

method proposed in Ref. [2] are quivalent, but in the case

of “long” diagrams (m

max

= 8), the diﬀerence between

these two methods becomes more signiﬁcant. When the

high-frequency atmospheric ﬂuctuation occurs, the alter-

native method is better than the former one; but if the

low-frequency atmospheric ﬂuctuation presents, the clas-

sic Langley method is preferable.

The interesting idea sugge sted in Ref. [6] is that similar

diagrams for three-wavelength photometer should have

an argument not for the optical air mass, but for the ad-

justable combination of optical thicknesses in three wave -

lengths. Adjusting the value of this combination as far as

zero, one can reach the wanted combination of solar con-

stants in three wavelengths. But this idea is signiﬁcant

only fo r multi-wavelength methods of sun pho tometry.

We describe a new calibration method fo r sun pho-

tometers which is also based on Bouguer-Beer Law. It

is assumed that the photometric ground measurements

are carried out at the wavele ngth λ by air mass m. In

this case, the intensity of solar radiation at the input of

photometer may be determined as

I (λ, m) = I

(λ) e

−mτ

, (4)

Fig. 1. Langley diagram for calibration of sun photometers.

1671-7694/2009/090760-04

 2009 Chinese Optics Letters

下载后可阅读完整内容，剩余3页未读，立即下载

weixin_38515362

粉丝: 3
资源: 945

基于Bouguer-Beer定律的太阳光谱仪新型校准方法

METHODOLOGY FOR THE DIGITAL CALIBRATION OF ANALOG CIRCUITS AND SYSTEMS

A new camera calibration method for robotic applications

Vector projection method used for calibration of the polarimeter module

Method for in situ calibration of multiple feedback interferometers

A three-spectrum method for accurate calibration of bi-plate zero-order retarder

Principal component analysis or kernel principal component analysis based joint spectral subspace method for calibration transfer

Expert System for Calibration of HSPF

Research on calibration method in lab of direct solar channels of Sun photometer

Constrained estimation for calibration of Stokes polarimeter in the presence of different noise

Techniques for Calibration of the Scale Factor and Image Center for High Accuracy 3D Machine Vision Metrology

最新资源