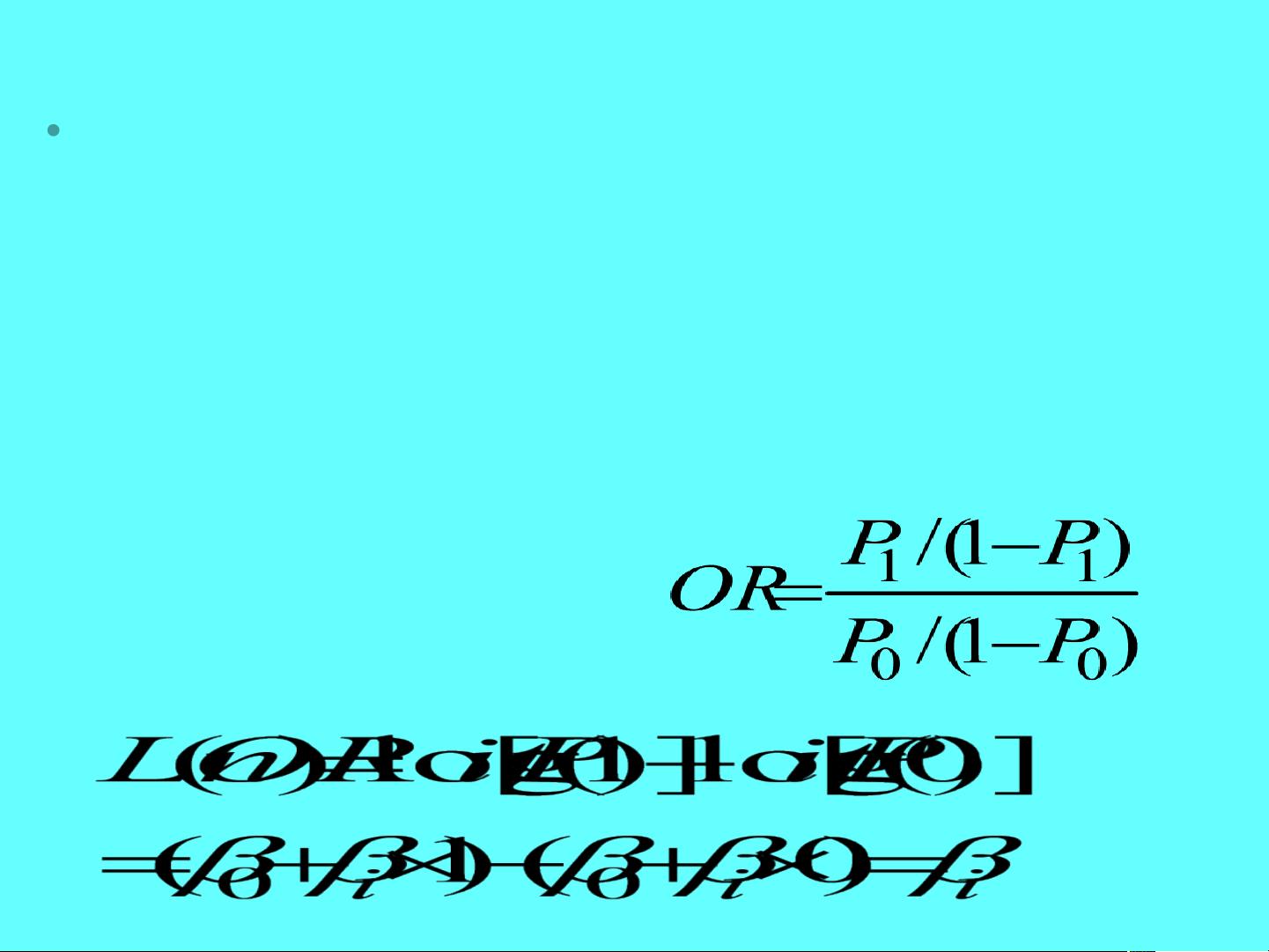"多元线性回归分析及应用研究"
115 浏览量
更新于2023-12-17
收藏 4.14MB PPTX 举报
Logistic回归分析及应用是一种常见的统计分析方法,在医学实践中经常应用。它可以解决一个应变量与多个自变量数量关系的问题。举例来说,医院住院人数不仅与门诊人数有关,还可能与病床周转次数、床位数等因素有关。类似地,儿童的身高不仅与遗传因素有关,还可能与生活质量、性别、地区、国别等因素有关。人的体表面积也可能与体重、身高等因素有关。
多元线性回归分析的数据结构如下表示:
表1 多元线性回归分析的数据结构
实验对象 y X1 X2 X3 …. XP
1 y1 a11 a12 a13 … a1p
2 y2 a21 a22 a23 … a2p
3 y3 a31 a32 a33 … a3p
… … … … … … …
n yn an1 an2 an3 … anp
在多元线性回归分析中,y是应变量,X1, X2, X3, ..., XP是自变量。实验对象从1到n表示有n个观察值。每个观察值包括一个应变量y和P个自变量X1, X2, X3, ..., XP的值。
多元线性回归模型的目标是通过实验测得的数据,建立一个数学模型来描述自变量和应变量之间的关系。这个关系通常被假设为线性关系,并且被用来预测或解释应变量的值。
然而,多元线性回归模型的假设不一定总能满足实际情况。特别是当应变量是一个二元变量时,多元线性回归模型就无法直接应用了。这时,我们可以使用Logistic回归分析来解决这个问题。
Logistic回归分析是一种常见的分类模型,可用于分析二元变量的结果。它使用logistic函数来建立自变量与二元变量之间的概率关系。该函数可以将自变量的线性组合映射到一个0到1之间的数值范围,表示事件发生的概率。
Logistic回归模型的数学表达式为:
P(Y=1|X) = e^(β0 + β1X1 + β2X2 + β3X3 + ... + βPXP) / (1 + e^(β0 + β1X1 + β2X2 + β3X3 + ... + βPXP))
其中,P(Y=1|X)表示在给定自变量X的条件下,应变量Y等于1的概率。β0, β1, β2, β3, ..., βP是待估计的回归系数。
通过最大似然估计等方法,可以推导出回归系数的估计值,并对模型进行拟合和推断。这样,我们可以通过Logistic回归模型来预测二元变量的概率,从而对事件的发生与否进行分类。
总之,Logistic回归分析是一种应对二元变量的常见统计分析方法。通过建立Logistic回归模型,我们可以探索自变量与二元变量之间的概率关系,实现对事件分类的预测和解释。在医学实践及其他领域中,Logistic回归分析具有广泛的应用前景。
点击了解资源详情
点击了解资源详情
327 浏览量
134 浏览量
166 浏览量
2021-10-01 上传
151 浏览量
2021-10-07 上传
144 浏览量
matlab大师
- 粉丝: 2865
最新资源
- Premiere Pro CS6视频编辑项目教程微课版教案
- SSM+Lucene+Redis搜索引擎缓存实例解析
- 全栈打字稿应用:演示项目实践与探索
- 仿Windows风格的AJAX无限级树形菜单实现教程
- 乐华2025L驱动板通用升级解决方案
- Java通过jcraft实现SFTP文件上传下载教程
- TTT素材-制造1资源包介绍与记录
- 深入C语言编程技巧与实践指南
- Oracle数据自动导出并转换为Excel工具使用教程
- Ubuntu下Deepin-Wine容器的使用与管理
- C语言网络聊天室功能详解:禁言、踢人与群聊
- AndriodSituationClick事件:详解按钮点击响应机制
- 探索Android-NetworkCue库:高效的网络监听解决方案
- 电子通信毕业设计:简易电感线圈制作方法
- 兼容性数据库Compat DB 4.2.52-5.1版本发布
- Android平台部署GNU Linux的新方案:dogeland体验